Сторінка
11

Методика навчання диференціальних рівнянь майбутніх вчителів математики в педагогічних університетах

Теорема 1. Якщо в рівнянні функція і її частинна похідна по у неперервні в деякій області D на площині 0ху, яка містить деяку точку , то існує єдиний розв'язок цього рівняння , який задовольняє умові при .

Геометричний зміст теореми полягає в тому, що існує і притім єдина функція , графік якої проходить через точку .

Означення 2. Умова, що при функція у повинна дорівнюватися заданому числу , називається початковою умовою, або умовою Коші. Вона записується у вигляді

або .

Означення 3. Задача, у якій потрібно знайти частинний розв'язок рівняння , який задовольняє початковій умові , називається задачею Коші.

Означення 4. Загальним розв'язком диференціального рівняння першого порядку називається функція

,

яка залежить від однієї довільної сталої С і задовольняє наступним умовам:

а) вона задовольняє диференціальному рівнянню при будь-якому конкретному значенні сталої С;

б) яка б не була початкова умова при , тобто , можна знайти таке значення , що функція задовольняє даній початковій умові. При цьому передбачається, що значення і належать до тієї області зміни змінних х і у, у якій виконуються умови теореми існування й одиничності розв'язку.

У процесі знаходження загального розв'язку диференціального рівняння ми приходимо до співвідношення вигляду

,

не розв'язаному відносно у. Розв'язавши це співвідношення відносно у, одержуємо загальний розв'язок. Однак не завжди удається виразити у в елементарних функціях; у таких випадках загальний розв'язок залишається в неявному вигляді.

Означення 5. Рівність вигляду , яка неявно задає загальний розв'язок, називається загальним інтегралом диференціального рівняння.

Означення 6. Частинним розв'язком називається будь-яка функція , яка утворюється з загального розв'язку , якщо в останньому довільної сталої С придати визначене значення . Співвідношення називається в цьому випадку частинним інтегралом рівняння.

З геометричної точки зору загальний інтеграл являє собою сімейство кривих на координатній площині, яке залежить від однієї довільної сталої С. Ці криві називаються інтегральними кривими даного диференціального рівняння. Частинному інтегралу відповідає одна крива цього сімейства, яка проходить через деяку задану точку площини.

Вирішити або проінтегрувати диференціальне рівняння - значить:

а) знайти його загальний розв'язок або загальний інтеграл (якщо початкові умови не задані) або

б) знайти той частинний розв'язок рівняння, який задовольняє заданим початковим умовам (якщо такі є).

Означення 7. Особливим розв'язком називається такий розв'язок, у всіх точках якого умова одиничності не виконується, тобто в будь-якому околі кожної точки особливого розв'язку існують принаймні дві інтегральні криві, які проходять через цю точку.

Особливі розв'язки не утворюються з загального розв'язку диференціального рівняння ні при яких значеннях довільної сталої С (у тому числі і при ).

2. Диференціальні рівняння із відокремлюючими змінними

Означення 8. Диференціальне рівняння типу

називають рівнянням із відокремлюючими змінними, тому що в цьому рівнянні змінні відокремлені, тобто при знаходиться тільки функція від х, а при - тільки функція від у.

Інтегруючи обидві частини цього рівняння, одержимо співвідношення, яке зв'язує розв'язок у, незалежну змінну х і довільну сталу С, тобто одержимо загальний інтеграл рівняння

.

Приклад. Знайти загальний розв'язок рівняння

.

Розв'язок. , ,

.

3. Диференціальні рівняння із змінними, які відокремлюються.

Означення 9. Диференціальні рівняння, у яких змінні можна відокремити за допомогою множення або ділення обох частин рівняння на той самий вираз, називаються диференціальними рівняннями із змінними, які відокремлюються.

Це рівняння виду

.

Воно може бути приведене до рівняння із відокремленими змінними шляхом ділення обох його частин на вираз :

, або

.

Приклад. Знайти загальний розв'язок рівняння

.

Розв'язок. Відокремлюючи змінні, знаходимо:

, .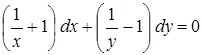