Сторінка
20

Методика навчання диференціальних рівнянь майбутніх вчителів математики в педагогічних університетах

Щоб визначити, яку підстановку вибирати – треба перевіряти.

Розв'язування задач.

Задача 1.

Вибираємо підстановку: .

Тоді .

Тому звідки:

Підставляємо:

III. Мета етапу: перевірка вмінь та навичок студентів розв’язувати однорідні диференціальні рівняння та рівняння з відокремлюючими змінними.

Самостійна робота (за варіантами). Перевіряється викладачем, результати оголошуються на наступному занятті.

Домашнє завдання: за підручником розв’язати на ст. 35 (P.L.1.4.) №1(15-21)

Практичне заняття 4

Тема: «Рівняння в повних диференціалах»

Мета:

вироблення вмінь та удосконалення навичок розв’язувати рівняння в повних диференціалах та рівняння, що зводяться до них;

вироблення вмінь зводити диференціальне рівняння до рівняння в повних диференціалах за допомогою інтегруючого множника;

розвиток продуктивного мислення;

виховання математичної культури.

При вивченні теми студенти повинні:

знати: означення інтегруючого множника, означення рівняння в повних диференціалах, методи його розв'язування;

уміти: застосовувати знання для розв'язування рівняння в повних диференціалах та рівняння, що зводиться до нього за допомогою інтегруючого множника;

здатні: розв'язувати рівняння в повних диференціалах.

Обладнання: підручники, дидактичний матеріал (таблиці), картки із самостійною роботою, мультимедійний проектор, комп’ютер.

Час: 2 год.

План заняття

I. Організаційний момент.

II. Вироблення вмінь та навичок.

III. Контроль.

Филиппов А.Ф. Сборник задач по обыкновенным дифференциальным уравнениям.

Хід заняття

I. Привітання із студентами, повідомлення мети й завдань заняття, перевірка присутніх, оголошення й аналіз результатів самостійної роботи.

II. Мета етапу: вироблення вмінь та удосконалення навичок розв’язувати рівняння в повних диференціалах та рівняння, що зводяться до них.

Розв’язування вправ.

Задача 1. Знайти загальний інтеграл диференціального рівняння першого порядку:

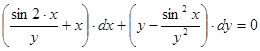
а) Перевіримо чи є це рівняння рівнянням в повних диференціалах вигляду P(x; y)dx + Q(x; y)dy = 0.

Якщо , а , то

, тобто

Таким чином, рівняння є рівнянням в повних диференціалах, де ліва частина представляє собою повний диференціал деякої функції F(х;у): dF(х; у) = dx + dy. Тобто , то

.

Із першого рівняння знайдемо: .

Диференціюємо по y та підставляємо в друге рівняння:

Тоді остаточно отримаємо:

Задача 2. Знайти загальний розв'язок диференціального рівняння.

Задача 3. Розв’язати методом інтегрувального множника.

, коли функція залежить від , то навпаки.

Умова не виконується. Робимо припущення, що існує множник .

Множимо на ліву та праву частини:

III. Мета етапу: перевірка вмінь та навичок студентів розв’язувати диференціальні однорідні та лінійні рівняння, рівняння з відокремлюючими змінними.

Самостійна робота (за варіантами). Перевіряється викладачем, результати оголошуються на здачі модуля (практичної частини).