Сторінка
5

Випуклість і вгнутість графіка функції, точки перегину. Асимптоти графіка функції

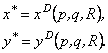Ці функції називаються функціями попиту. Зміст цього визначення полягає в тому, що споживач прагне до найбільшого задоволення від куплених ним товарів при обмежених доходах. З геометричної точки зору множина - трикутник з вершинами (рис.6.24 ). Як правило, функція зростає при збільшення і , тому найбільше її значення досягається на відрізку тобто споживач витрачає на покупки весь свій дохід. Функції є однорідними функціями нульового виміру. Отже, для диференційованої функції попиту виконуються тотожності Ейлера:

Як правило, графік функції корисності є строго вгнутий. В цьому випадку умови Куна-Таккера дають можливість знайти функцію попиту. Нехай множники Лагранжа, причому відповідає обмеженню нерівності нерівності Тоді функція Лагранжа запишеться так:

Умови Куна-Таккера для функції будуть такими:

Якщо наперед відомо, що функція попиту не перетворюється в нуль, то із четвертого і п’ятого рівнянь системи випливає, що В цьому випадку система буде простішою

Якщо або то із перших двох рівнянь системи випливає, що Але тоді можна виключити із системи. В результаті отримаємо систему рівнянь