Сторінка
1

Існування та єдиність розв’язків диференціальних рівнянь першого порядку. Неперервна залежність та диференційованість

Клас диференціальних рівнянь, що інтегруються в квадратурах, досить невеликий, тому мають велике значення наближені методи розв’язку диференціальних рівнянь. Але, щоб використовувати ці методи, треба бути впевненим в існуванні розв’язку шуканого рівняння та в його єдиності.

Зараз значна частина теорем існування та єдиності розв’язків не тільки диференціальних, але й рівнянь інших видів доводиться методом стискуючих відображень.

Визначення. Простір називається метричним, якщо для довільних двох точок визначена функція , що задовольняє аксіомам:

1., причому тоді і тільки тоді, коли ;

2. (комутативність);

3. (нерівність трикутника).

Функція називається відстанню в просторі (метрикою простору ).

Приклад 1.6.1. Векторний - вимірний простір .

Нехай . За метрику можна взяти: , .

Приклад 1.6.2. Простір неперервних функцій на відрізку позначається - . За метрику можна взяти

Визначення. Послідовність називається фундаментальною, якщо для довільного існує таке, що при і довільному буде .

Визначення. Метричний простір називається повним, якщо довільна фундаментальна послідовність точок простору збігається до деякої точки простору .

Теорема (принцип стискуючих відображень). Нехай в повному метричному просторі задано оператор , що задовольняє умовам.

1. Оператор переводить точки простору в точки цього ж простору, тобто якщо , то і .

2. Оператор є оператором стиску, тобто

, де - довільні точки .

Тоді існує єдина нерухома точка , яка є розв’язком операторного рівняння і вона може бути знайдена методом послідовних відображень, тобто , де , причому , вибирається довільно.

Доведення. I. Візьмемо довільну точку і побудуємо послідовність . Покажемо, що побудована послідовність є фундаментальною. Дійсно

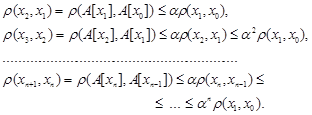
Оцінимо . Застосувавши -разів пра­вило трикутника, отримуємо

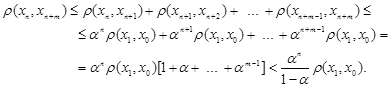
Таким чином . И при достатньо великому : , тобто послідовність є фундаментальною і, в силу повноти простору , збігається до деякого елемента цього ж простора .

II. Покажемо, що є нерухомою точкою, тобто .

Нехай від супротивногоі . Застосувавши правило трикутника, одержимо .Оцінимо кожний з доданків.

1) Оскільки , то при буде.