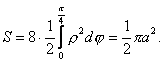|
План - Схеми застосування інтеграла до знаходження геометричних і фізичних величин
- Обчислення площі плоскої фігури
- Обчислення площі в декартових координатах
- Площа криволінійного сектора в полярних координатах
ЗАСТОСУВАННЯ ВИЗНАЧЕНОГО ІНТЕГРАЛА
1. Площа плоскої фігури
1.1. Обчислення площі в декартових координатах В п.9.2. мова йшла про те, коли розглядається площа криволінійної трапеції, обмеженої віссю  кривою кривою 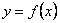 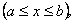 причому причому 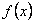 на відрізку на відрізку  може бути як додатною, так і від’ємною, то площа такої криволінійної трапеції обчислюється за формулою може бути як додатною, так і від’ємною, то площа такої криволінійної трапеції обчислюється за формулою 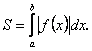 (10.1) Нехай у прямокутній системі координат фігура (10.1) Нехай у прямокутній системі координат фігура  (рис.10.1) обмежена кривими (рис.10.1) обмежена кривими 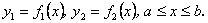 Виділимо у фігурі смужку шириною Виділимо у фігурі смужку шириною  . Її довжина дорівнюватиме . Її довжина дорівнюватиме  . Тоді площа смужки . Тоді площа смужки 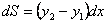 . Звідси . Звідси 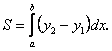 Отже, Отже, 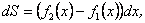 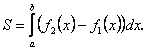 (10.2) (10.2)
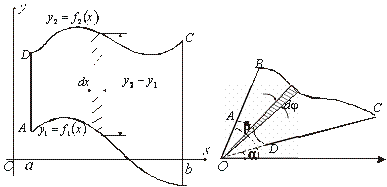 Рис.10.1 Рис.10.2 Обчислимо тепер площу криволінійної трапеції у випадку, коли крива задана рівняннями в параметричній формі Рис.10.1 Рис.10.2 Обчислимо тепер площу криволінійної трапеції у випадку, коли крива задана рівняннями в параметричній формі
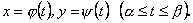 (10.3) Нехай рівняння (10.3) визначають деяку функцію (10.3) Нехай рівняння (10.3) визначають деяку функцію 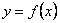 на відрізку на відрізку  а тому площа криволінійної трапеції може бути обчислена за формулою а тому площа криволінійної трапеції може бути обчислена за формулою
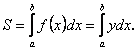 Зробивши заміну в цьому інтегралі Зробивши заміну в цьому інтегралі 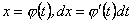 і враховуючи, що і враховуючи, що 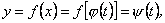 одержимо одержимо 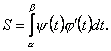 (10.4) (10.4)
1.2. Площа криволінійного сектора в полярних координатах Нехай криві, що обмежують фігуру, задані рівнянням в полярній системі координат і відрізками двох полярних радіусів (рис. 10.2) .Знайдемо площу фігури  якщо: якщо: 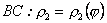 , , 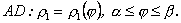 У фігурі У фігурі  виділимо сектор з центральним кутом виділимо сектор з центральним кутом  Вважатимемо, що дуги, які обмежують сектор Вважатимемо, що дуги, які обмежують сектор  , є дугами кіл радіусів , є дугами кіл радіусів  . Очевидно, що площа сектора . Очевидно, що площа сектора  між дугами між дугами  i i  дорівнює дорівнює 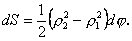 Інтегруючи, одержимо Інтегруючи, одержимо 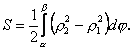 (10.5) Приклад 1. Знайти площу фігури, обмеженої гіперболою (10.5) Приклад 1. Знайти площу фігури, обмеженої гіперболою 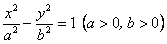 , віссю , віссю  і прямою, яка з’єднує точку і прямою, яка з’єднує точку 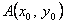 , що лежить на гіперболі, з початком координат. Р о з в ’ я з о к. З рівняння гіперболи маємо , що лежить на гіперболі, з початком координат. Р о з в ’ я з о к. З рівняння гіперболи маємо
 Щоб знайти площу заштрихованої на рис.10.3 фігури, досить знайти площу фігури Щоб знайти площу заштрихованої на рис.10.3 фігури, досить знайти площу фігури  , а потім від площі трикутника , а потім від площі трикутника  відняти площу фігури відняти площу фігури  . Отже, . Отже, 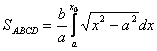 . Найкращим методом для обчислення цього інтеграла є інтегрування частинами. В результаті інтегрування дістанемо . Найкращим методом для обчислення цього інтеграла є інтегрування частинами. В результаті інтегрування дістанемо   Оскільки Оскільки  то то  . Цікаво, що цю площу можна записати у вигляді . Цікаво, що цю площу можна записати у вигляді
 Рис.10.3 Рис.10.4 Рис.10.3 Рис.10.4
 , де , де  - функція, обернена відносно функції - функція, обернена відносно функції  . Пропонується переконатися в цьому самостійно. Приклад 2. Знайти площу фігури, обмеженої кривою . Пропонується переконатися в цьому самостійно. Приклад 2. Знайти площу фігури, обмеженої кривою
 . Р о з в ’ я з о к.Перейшовши в цьому рівнянні до прямокутної системи координат, легко встановити, що відповідна крива є центрально-симетричною відносно системи координат. Крім того, із заданого рівняння видно, що . Р о з в ’ я з о к.Перейшовши в цьому рівнянні до прямокутної системи координат, легко встановити, що відповідна крива є центрально-симетричною відносно системи координат. Крім того, із заданого рівняння видно, що  , тобто крива повністю знаходиться всередині кола радіуса , тобто крива повністю знаходиться всередині кола радіуса  з центром в початку координат, що дотикається вона до кола лише в точках з центром в початку координат, що дотикається вона до кола лише в точках  , проходить через початок координат при , проходить через початок координат при  , дотикаючись до прямих , дотикаючись до прямих  . Отже графік заданої функції має вигляд чотирипелюсткової троянди (рис. 10.4). Очевидно, що для обчислення площі досить знайти площу заштрихованої фігури і потім її помножити на 8. Отже, . Отже графік заданої функції має вигляд чотирипелюсткової троянди (рис. 10.4). Очевидно, що для обчислення площі досить знайти площу заштрихованої фігури і потім її помножити на 8. Отже, 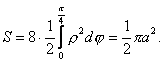
|

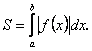 (10.1) Нехай у прямокутній системі координат фігура
(10.1) Нехай у прямокутній системі координат фігура 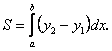 Отже,
Отже, 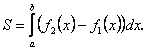 (10.2)
(10.2)
 Рис.10.1 Рис.10.2 Обчислимо тепер площу криволінійної трапеції у випадку, коли крива задана рівняннями в параметричній формі
Рис.10.1 Рис.10.2 Обчислимо тепер площу криволінійної трапеції у випадку, коли крива задана рівняннями в параметричній формі
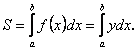 Зробивши заміну в цьому інтегралі
Зробивши заміну в цьому інтегралі 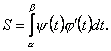 (10.4)
(10.4)
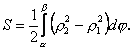 (10.5) Приклад 1. Знайти площу фігури, обмеженої гіперболою
(10.5) Приклад 1. Знайти площу фігури, обмеженої гіперболою 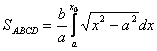 . Найкращим методом для обчислення цього інтеграла є інтегрування частинами. В результаті інтегрування дістанемо
. Найкращим методом для обчислення цього інтеграла є інтегрування частинами. В результаті інтегрування дістанемо  Рис.10.3 Рис.10.4
Рис.10.3 Рис.10.4