• Головна

Сторінка
5

Вирівнювальні обчислення в тріангуляції

Реферати / Географія фізична, геологія, геодезія / Вирівнювальні обчислення в тріангуляції

Розглянемо виведення умовного рівняння для ординат. Для цього випадку рівняння зв’язку має вигляд

 

(2.105)

Значення величини Sij та αij обчислюють за формулами (2.99) та (2.100).

Підставивши в формулу (2.105) замість найймовірніших значень величин Sij та αij їх значення, отримані по виміряним кутам, маємо

 

(2.106)

Визначимо коефіцієнти при поправках в кути з врахуванням формул (2.99), (2.100). Маємо

.

(2.107)

З врахуванням формул (2.106) і (2.107) рівняння поправок має вигляд

 

(2.108)

Розділивши всі члени рівняння (2.108) на величину k·10n, де k і n підбирають таким чином, щоб коефіцієнти при поправках були близькі до одиниці. Маємо

 

.

(2.109)

Про допустимі значення вільних членів умовних рівнянь

Для оцінки якості виміряних кутів проводять підрахунок граничних (допустимих) значень вільних членів умовних рівнянь.

При заданій довірчій ймовірності Р гранична помилка

 

M=m · t,

(2.110)

де

m — середня квадратична помилка виміряних кутів;

t — коефіцієнт, який знаходять за виразом

 

.

(2.111)

При достатньо великому числі вимірів n величину відповідно критерію Шовене находять за формулою

 

.

(2.112)

Таким чином, знаючи величину можна знайти величину t за формулою (2.111). Для знаходження величини t існують спеціальні таблиці.

В реальних випадках при числі трикутників в тріангуляції 12–16 значення величини t коливаються незначно і t≈2,5. На основі цього (2.110) буде

 

.

(2.113)

Запишемо умовне рівняння для фігури

 

.

(2.114)

Переходячи до нормального рівняння маємо

 

,

(2.115)

де .

Із (2.155) маємо

 

.

(2.116)

При вирівнювання повинна задовольнятися вимога

 

.

(2.117)

Відомо, що

 

.

(2.118)

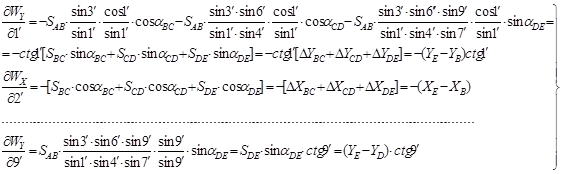Завантажити реферат Завантажити реферат
Перейти на сторінку номер:
 1  2  3  4  5  6  7  8  9  10  11 


Інші реферати на тему «Географія фізична, геологія, геодезія»: