Сторінка
1
На сьогодні в країнах колишнього союзу, в тому числі й в Україні, діє нормативний документ по розрахунках максимальних витрат води на річках, який було запропоновано ще в 1972 році, а потім дещо змінено в 1983 році. Фахівцями неодноразово на авторитетних конференціях і симпозіумах приверталася увага розробників на невідповідність у багатьох випадках розрахункових максимумів паводків і повеней матеріалам спостережень, особливо у випадках, коли місцеві особливості формування стоку суттєво відрізняються від фонових. Удосконалення діючої нормативної бази не можливо в принципі – через емпіричний підхід при її створенні. Досить звернутися до відомих базових структур БНіПу, щоб переконатися в цьому.
Так, для весняної повені (без наведення поправок) використовується формула [7]:
, (1)
де qm – максимальний модуль повені, ko – коефіцієнт “дружності” повені, Ym – розрахунковий шар стоку, F – площа водозбору, Fo – додаткова площа, за допомогою якої ураховується зменшення інтенсивності редукції на малих водозборах.
Згідно з дослідженнями [4], чисельник є максимальний модуль схилового стоку q¢m, тоді
. (2)
Коефіцієнт редукції максимального модуля qm/q¢m дорівнює
. (3)
Його верхньою фізичною границею повинно бути qm/q¢m=1.0 при F®0. Але якщо з цього боку розглянути (3), то легко переконатись, що при F®0
, (4)
за винятком, коли Fо=1.0.
З структури (1) не ясно, до котрого з параметрів (ko чи Ym) відносяться поправки на залісеність та заболоченість. При розрахунках дощових паводків в залежності від розмірів водозбірних площ використовується не одна, а дві формули (зауважимо, що їх “склеювання” не забезпечується:
а) при F>100-200 км2
; (5)
б) при F<100-200 км2
, (6)
де 
- ординати кривих редукції середньої інтенсивності опадів у часі, Н1% - добовий максимум опадів, h - коефіцієнт стоку.
У теоретичному відношенні (5) взагалі ну відповідає фізичним вимогам до граничних значень qm, бо qm/q¢m дорівнює одиниці не за умови F®0, а при F=200 км2. Вважаємо, що більш обгрунтованим було б (5) записати у загальному вигляді
. (7)
Щодо функції 
, то вона використовується помилково, бо як показано в [3], замість неї в (6)повинна входити інша величина, а саме:
, (8)
де (n+1)/n – коефіцієнт нерівномірності схилового припливу, То – тривалість схилового припливу, tp – час руслового добігання паводкових хвиль.
Таким чином, використана (майже безпідстевно) в СНіПі функція 
тотожня осередненому в межах tp коефіцієнту повноти схилового припливу
. (9)
Наведене вище дає змогу прийти до висновку про суттєві недоліки структурного плану в діючому БНіПі 2.01.14-83 і необхідність розробки більш досконалої нормативної бази, яка б відповідала світовим досягненням сучасної гідрології, а саме головне – достовірно описувала процеси трансформації схилового припливу в русловий стік.
Як на думку авторів, побудувати розрахункову схему для визначення максимальних витрат води під час паводків чи повіней досить надійно можна, виходячи із рівняння руслових ізохрон
, (10)
де fi – міжізохронні площі, eі – коефіцієнти русло-заплавного регулювання в межах міжізохронних ділянок.
Максимальна витрата води буде дорівнювати:
а) за tp<To
, (11)
де 
- шар стоку, найбільший у межах tp, тобто
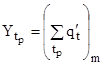, (12)
k1 – гідрографічний коефіцієнт, який співпадає з раніше запропонованим А.М.Бефані [1]
; (13)
б) за tp³To
, (14)
де V – швидкість руху паводкових хвиль в руслах, k2 – гідрографічний коефіцієнт
. (15)
Вирази (11) і (14) можна узагальнити у вигляді
. (16)
Рівняння (16) вперше було отримано А.М.Бефані [1], який реалізував модель руслових ізохрон, виходячи з передумов що: 1)коефіцієнт щільності руслової мережі залишається незмінним в межах річкових водозборів; 2)русло-заплавне регулювання відбувається однаково на різних ділянках річкової мережі. Але, як відомо, це не зовсім так – на малих водозборах і розгалужених річкових системах процеси регулювання паводків мають свої особливості. Вони полягають в тім, що при зростанні водозбірних площ відбувається закономірне і поступове збільшення відношення ширини річки до її середньої глибини.
Завантажити реферат