Сторінка
2

Метод зведення визначника до трикутного вигляду

D = .

У даному визначнику четвертий елемент четвертого стовпчика не дорівнює нулю. Тому можна від п’ятого рядка відняти четвертий, помножений на і одержати визначник трикутного вигляду відносно головної діагоналі

D = .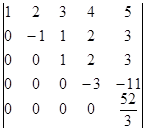

Тоді D = 1×(-1)×1×(-3)× = 52

На практиці рекомендується при обчисленні визначників з цілими елементами на кожному кроці одержувати визначники також з цілими елементами. У нашому випадку перед виконанням останнього кроку перетворень можна було, наприклад, перейти від визначника

D =

до визначника

D =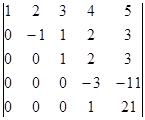

відніманням від п’ятого рядка четвертого, помноженого на 2. Далі переставимо четвертий і п’ятий рядки. Як відомо, при цьому змінюється знак визначника:

D = ‑ .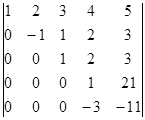

Нарешті до п’ятого рядка додамо четвертий, помножений на 3:

D = ‑ .

Таким чином, D = ‑ (1×(-1)×1×1× 52) = 52.

Розглянемо тепер деякі приклади обчислення визначників n–го порядку методом зведення до трикутного вигляду. При обчисленні визначників n–го порядку будемо суттєво користуватись закономірностями в будові цих визначників.

Приклад 2. Обчислити визначник

D = .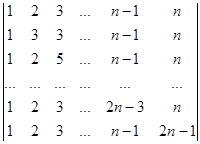

Розв’язування. Зрозуміло, що порядок визначника дорівнює n (наприклад, у першому рядку елементами є всі натуральні числа від 1 до n, кількість їх дорівнює n). Кожен рядок визначника, починаючи з другого, відрізняється від першого рядка лише єдиним елементом, а саме елементом, який стоїть на головній діагоналі. Тому можна від кожного рядка, починаючи з другого, відняти перший рядок. Одержуємо

D = .

Всі елементи одержаного визначника, що знаходяться нижче головної діагоналі, дорівнюють нулю. Таким чином, ми одержали визначник трикутного вигляду відносно головної діагоналі, а тому

D = 1×1×2× .×(n-2)×(n-1) = (n-1)!

Приклад 3. Обчислити визначник порядку n

D = .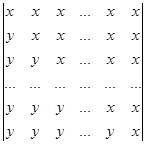

Розв’язування. В цьому визначнику всі елементи, яки знаходяться вище головної діагоналі, а також всі елементи головної діагоналі однакові. Визначник можна звести до трикутного вигляду відносно головної діагоналі, одержуючи нулі вище діагоналі. Віднімемо від першого рядка визначника другий. Одержуємо

D = .

Далі, аналогічно від другого рядка віднімемо 3-й, від 3-го ‑ 4-й і нарешті, від (n –1)-го – n-й.

D = .

Порядок визначника дорівнює n, а тому

D = x×(x-y)n-1.

Приклад 4. Обчислити визначник

D =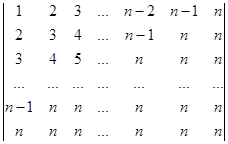

Розв’язування. Порядок визначника дорівнює n (елементи першого рядка – всі натуральні числа від 1 до n, тобто кількість їх дорівнює n). Всі елементи визначника на побічній діагоналі і нижче побічної діагоналі однакові. Тому визначник можна звести до трикутного вигляду відносно побічної діагоналі. Для цього віднімемо від n-го стовпчика визначника (n-1)-й стовпчик.

D = .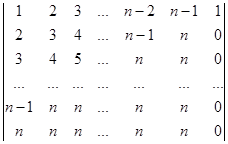

В останньому стовпчику залишається лише один ненульовий елемент. Далі аналогічно від (n-1)-го стовпчика віднімемо (n-2)-й, від (n-2)-го ‑ (n-3)-й і, нарешті, від 2-го стовпчика віднімемо 1-й. Одержуємо визначник трикутного вигляду відносно побічної діагоналі

D = .

Порядок визначника дорівнює n, а тому

D =

Приклад 5. Обчислити визначник

D = .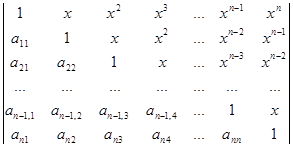

Розв’язування. Зрозуміло, що порядок визначника дорівнює n+1 (у першому рядку елементами є степеня змінної x від 0 до n). Будемо зводити визначник до трикутного вигляду відносно головної діагоналі. Неважко переконатись в тому, що елементи першого рядка, починаючи з другого, можна одержати помноженням відповідних елементів другого рядка на x. Тому, віднімаючи від першого рядка другий рядок, помножений на x, одержимо на місці цих елементів нулі. Тобто,

D = .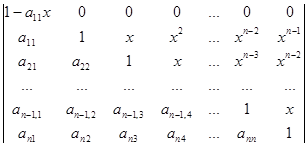

Далі, аналогічно, від другого рядка віднімемо 3-й, помножений на x, від 3-го рядка віднімемо 4-й, помножений на x, і нарешті від (n-1)–го рядка віднімемо n–й, помножений на x: