Сторінка
4
Розв’язування. Зрозуміло, що порядок визначника дорівнює n (число елементів на побічній діагоналі дорівнює n). Віднімемо перший рядок від всіх інших рядків
D =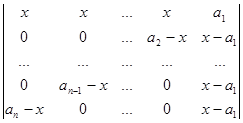 .
.
У цьому визначнику всі елементи n-го стовпчика, починаючи з другого, дорівнює x-a1. Будемо перетворювати визначник так, щоб всі елементи побічної діагоналі, починаючи з другого, були рівними 1. Для цього з першого стовпчика винесемо множник (an-x), з другого - (an-1-x), нарешті з (n-1)-го – множник (a2-x).
D = (an-x) (an-1-x) . (a2-x)  .
.
Далі з останнього стовпчика визначника віднімемо суму всіх інших стовпчиків, помножених на (x-a1). Одержуємо визначник трикутного вигляду відносно побічної діагоналі
D = (an-x) (an-1-x) . (a2-x)  .
.
Оскільки порядок визначника дорівнює n,
D = ![]() (an-x) (an-1-x) . (a2-x)
(an-x) (an-1-x) . (a2-x) 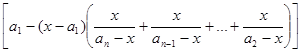 =
=
= ![]() (an-x)(an-1-x) .(a2-x)
(an-x)(an-1-x) .(a2-x) =
=
= ![]() x(a1-x)(a2-x)…(an-1-x)(an-x)
x(a1-x)(a2-x)…(an-1-x)(an-x) 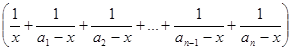 .
.
Приклад 11. Обчислити визначник
D = 
Розв’язування. Зрозуміло, що порядок визначника дорівнює n+1 (у першому рядку (n+1) елементів). Будемо зводити визначник до трикутного вигляду відносно головної діагоналі. Для цього будемо перетворювати визначник таким чином, щоб одержати визначник, всі елементи якого, що знаходяться нижче головної діагоналі, дорівнюють 0. Зрозуміло, якщо до першого стовпчика визначника додати другий, то на другому місці у першому стовпчику з’являється 0, але на третьому місці замість 0 з’являється –x. Таким чином, слід додати ще третій стовпчик. Тобто, для того, щоб у першому стовпчику всі елементи, починаючи з другого, були рівними нулю, слід додати до першого стовпчика суму всіх інших стовпчиків. Одержуємо
D =  .
.
Далі, аналогічно, до 2-го стовпчика додаємо всі стовпчики, починаючи з 3-го, до 3-го – всі стовпчики, починаючи з 4-го, і нарешті до n-го стовпчика додамо останній. Одержуємо визначник трикутного вигляду відносно головної діагоналі.
D = 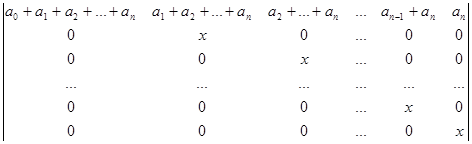 .
.
Оскільки порядок визначника дорівнює n+1, одержуємо:
D = (a0+a1+a2+…+an)xn.
Задачі для самостійного розв’язування
Обчислити визначники методом зведення до трикутного вигляду
1. 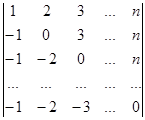
2. 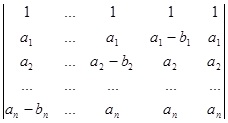
3. 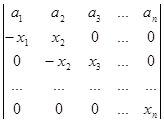
4. 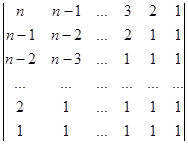
5.  (порядок визначника дорівнює n)
(порядок визначника дорівнює n)
6.  (порядок визначника дорівнює n)
(порядок визначника дорівнює n)
7. 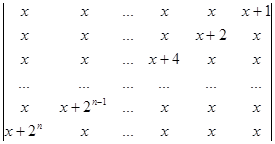
Інші реферати на тему «Математика»:
Комплексні числа, їх зображення на площині. Алгебраїчна, тригонометрична і показникова форми комплексного числа
Відповідності, функції, відображення
Лінійні диференціальні рівняння вищих порядків
Монотонність функції, необхідні і достатні умови. Eкстремум функції однієї та декількох змінних
Елементи логіки
