Сторінка
3

Метод зведення визначника до трикутного вигляду

D = .

Всі елементи визначника, що знаходяться вище головної діагоналі, дорівнюють нулю. Таким чином, ми одержали визначник трикутного вигляду відносно головної діагоналі і

D = (1- a11x)(1-a22x)(1-a33x)…(1-annx)×1 =

Приклад 6. Обчислити визначник порядку n

D = .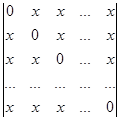

Розв’язування. У визначниках такого вигляду зручно на першому кроці від кожного рядка, починаючи з другого, відняти перший рядок. Одержуємо визначник

D = .

Далі визначник неважко звести до трикутного вигляду відносно головної діагоналі. Для цього можна, наприклад, додати до першого стовпчика суму всіх інших стовпчиків. Згідно з властивостями визначника, його величина при цьому не змінюється. Одержуємо визначник трикутного вигляду відносно головної діагоналі.

D = .

Порядок визначника дорівнює n, а тому

D = (n-1)×x×(-x)n-1 = (-1)n-1(n-1)xn.

Визначник можна зводити до трикутного вигляду різними способами. Наприклад, для даного визначника можна запропонувати ще один спосіб зведення. Неважко бачити, що у початковому визначнику сума елементів кожного рядка і кожного стовпчика однакова. Тому додамо до першого рядка початкового визначника суму всіх інших рядків. При цьому величина визначника не змінюється

D = .

Перший рядок визначника складається з однакових елементів, а тому з цього рядка можна винести множник за знак визначника

D = (n-1)x.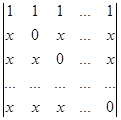

Далі одержуємо нулі нижче головної діагоналі. Для цього достатньо відняти від всіх рядків визначника, починаючи з другого, перший рядок, помножений на x.

D = (n-1)x.

Одержали визначник трикутного вигляду відносно головної діагоналі.

D = (n-1)×x×(-x)n-1 = (-1)n-1(n-1)xn.

Приклад 7. Обчислити визначник порядку n

D = .

Розв’язування. Помножимо перший рядок визначника на x. З властивостей визначників випливає, що при цьому визначник помножається на x, тобто

D = .

Далі аналогічно помножуємо перший стовпчик визначника на x. Визначник помножається на x ще один раз

D = .

Одержуємо визначник, який співпадає з визначником з попереднього прикладу. У цьому визначнику від всіх рядків, починаючи з другого, віднімаємо перший рядок:

D = .

Далі до першого стовпчика додамо суму всіх інших стовпчиків

D = .

Одержуємо визначник трикутного вигляду відносно головної діагоналі, а тому

D = (n-1)x×(-x)n-1=(-1)n-1(n-1)xn = (-1)n-1(n-1)xn-2.

Приклад 8. Обчислити визначник

D = .

Розв’язування. Зрозуміло, що порядок визначника дорівнює n (на головній діагоналі n елементів). Будемо перетворювати визначник таким чином, щоб одержати визначник, всі елементи головної діагоналі якого дорівнюють 1. Для цього з другого стовпчика визначника винесемо множник – число 2, з третього – множник 3, і нарешті з останнього – множник n. Одержуємо

D =2×3×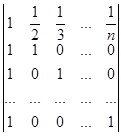 .×n×= n!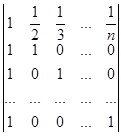

В одержаному визначнику всі елементи першого стовпчика, починаючи з другого, співпадають з відповідними елементами головної діагоналі. Тому, віднімаючи від першого стовпчика суму всіх інших стовпчиків, одержуємо визначник трикутного вигляду відносно головної діагоналі

D =n! .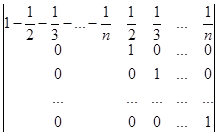

Таким чином,

D = n!(1-)

Приклад 9. Обчислити визначник

D = .

Розв’язування. Порядок визначника дорівнює n (число елементів на головної діагоналі дорівнює n). У цьому визначнику можна відняти перший рядок від всіх інших рядків. D = .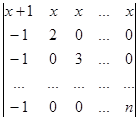

Звертаємо увагу на те, що всі елементи першого стовпчика одержаного визначника, починаючи з 2-го дорівнюють –1. Тому перетворюємо визначник так, щоб діагональні елементи, починаючи з 2-го, були рівними 1. Для цього з другого стовпчика виносимо множник – число 2, з третього – число 3, і нарешті з n-го – число n:

D = 2×3×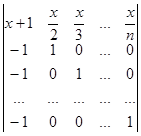 .×n×= n!×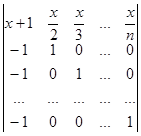

В одержаному визначнику до першого стовпчика додаємо суму інших стовпчиків:

D = n!× .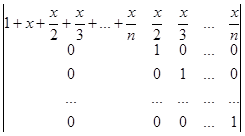

Одержуємо визначник трикутного вигляду відносно головної діагоналі. Тому

D = n!(1+x+).

Приклад 10. Обчислити визначник

D =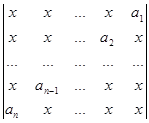.