Сторінка
4

Функціональний ряд, область його збіжності. Cтепеневі ряди. Теорема Абеля

Рис.13.3

Якщо , то степеневий ряд збігається тільки в одній точці Якщо , то ряд збігається на всій числовій осі.

Вкажемо метод визначення радіуса збіжності степеневого ряду (13.39). Для цього розглянемо ряд, складений із абсолютних величин його членів:

(13.43)

Застосуємо ознаку Даламбера

,

де Тоді за ознакою Даламбера ряд (13.43) збігається, якщо , тобто якщо , і розбігається, якщо , тобто якщо

Отже, ряд (13.39) збігається абсолютно при і розбігається при За означенням 2 інтервал є інтервалом збіжності степеневого ряду (13.39), тобто

(13.44)

Аналогічно для визначення інтервалу збіжності можна користуватися радикальною ознакою Коші, і тоді радіус збіжності

(13.45)

2.2. Ряди за степенями

Степеневий ряд, розташований за степенями має такий вигляд :

(13.46)

де постійні також називаються коефіцієнтами ряду.

При ми одержимо ряд (13.39), а тому ряд (13.39) є частинним випадком ряду (13.46).

Для визначення області збіжності ряду (13.46) проведемо в ньому заміну змінної

після чого одержимо ряд типу (13.39), розташований за степенями

(13.47)

Нехай інтервал є інтервал збіжності ряду (13.47). Звідси випливає, що ряд (13.46) буде збігатися при значеннях що задовольняють нерівність тобто або

(13.48)

Оскільки ряд (13.47) розбігається при то ряд (13.46) буде розбігатися при тобто буде розбігатися поза інтервалом (13.48).

Отже, інтервалом збіжності степеневого ряду (13.46) буде інтервал з центром в точці Всі властивості степеневого ряду, розташованого за степенями всередині інтервалу збіжності повністю зберігаються для степеневого ряду, розташованого за степенями всередині інтервалу збіжності

Приклад.

Р о з в ‘ я з о к. За формулою (2.30) одержимо

При : Це знакочергуючий ряд.

Перевіримо умови теореми Лейбніца:

1)

2) Оскільки умови теореми виконуються,

то даний знакочергуючий ряд збігається.

При : Це ряд з додатними членами.

Для дослідження його збіжності використаємо інтегральну ознаку Коші 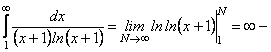інтеграл розбігається, тому і ряд розбігається. Отже, область збіжності даного ряду