Сторінка
5

Диференціальні рівняння першого порядку (з відокремлюваними змінними, однорідні, лінійні, Бернуллі)

Таким чином, загальний розв’язок має вигляд

.

б) Цей же самий результат отримаємо, застосувавши до початкового рівняння підстановку :

або .

Знайдемо з рівняння . Відокремимо змінні: , звідки . Запишемо рівняння відносно , звідси . Отже загальний розв’язок (довільна стала ) збігається як слід було чекати, із розв’язком, знайденим раніше.

Приклад 2. При відстоюванні суспензії має місце повільне осідання твердих частинок під дією сили ваги , якщо опір середовища пропорційний швидкості осідання частинок, що осідають в рідині без початкової швидкості.

Р о з в ’ я з о к. Згідно з законом Ньютона, де маса частинки; швидкість її руху; час; сила дії на частинку. Враховуючи умову задачі, маємо , де вага частинки; сила опору; коефіцієнт пропорційності. Отже, відносно швидкості руху дістаємо рівняння

,

або , причому .

Це лінійне диференціальне рівняння першого порядку. Щоб знайти його частинний розв’язок, що задовольняє початковій умові , спочатку відшукаємо загальний розв’язок рівняння. Використаємо метод варіації довільної сталої. Відповідне однорідне рівняння має вигляд

.

Після відокремлювання змінних та інтегрування отримаємо

, звідки .

Щоб знайти загальний розв’язок рівняння з правою частиною, вважаємо, що в останній рівності .

Тоді ,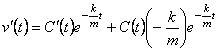

і відносно одержується, згідно з умовою, таке рівняння:

,або.

Звідси ,

де довільна стала. Інтегруючи, маємо

.

Тоді загальний розв’язок рівняння набуває вигляду

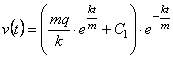,або .

Поклавши тут і , знайдемо, що .

Отже, частинний розв’язок поставленої задачі матиме вигляд

.

Приклад 3. З фізики відома залежність між силою стуму та електрорушійною силою в колі, яке має опір та самоіндукцію ( та - сталі):

.

Якщо , то це рівняння повністю збігається з диференціальним рівнянням, розглянутим у прикладі 2, хоч описувані процеси зовсім різні.

Нехай . Тоді відносно маємо диференціальне рівняння, яке зручно записати у вигляді

.

Знайдемо загальний розв’язок цього лінійного рівняння. Нехай , де та - невідомі функції. Тоді Після підстановки в рівняння та маємо:

або .

Невідому функцію знайдемо з рівняння