Сторінка
2

Диференціальні рівняння першого порядку (з відокремлюваними змінними, однорідні, лінійні, Бернуллі)

Рис.12.1

Приклад 2 . Нехай відомо, що швидкість хімічної реакції, яка перетворює речовину на речовину , пропорційна добуткові концентрації цих речовин.

Потрібно скласти диференціальне рівняння залежності об’єму речовини від часу .

Нехай об’єм речовини , що бере участь в реакції, дорівнює . Тоді загальний об’єм . Приріст у разі переходу речовини в речовину має вигляд: , а швидкість реакції буде . Згідно з умовою

(12.10)

(коефіцієнт пропорційності), оскільки та - концентрації речовин та Враховуючи, що рівняння (12.10) запишемо у вигляді

або

(12.11)

де .

Цікаво відзначити, що рівняння (12.11) збігалося з рівнянням (12.5). Вперше таке рівняння використано у 1845 р. і названо як рівняння Ферхольста - Перла, застосовувалось воно для опису динаміки чисельності популяції в біології. Зауважимо, що такий самий вигляд мають рівняння інших процесів – наприклад, попиту на сезонні масові послуги на підприємствах побутового обслуговування, а також випаровування вологи з пористої речовини тощо.

Розглянемо диференціальне рівняння виду . Виявляється, що це рівняння також описує зовсім різні явища, процеси: при отримуємо закон органічного росту, при - рівняння процесу радіоактивного розпаду, залежності атмосферного тиску від висоти, процесу розряду конденсатора через опір й ін.

12.3. Однорідні диференціальні рівняння першого порядку і рівняння, що зводяться до однорідних

Рівняння першого порядку

називається однорідним відносно та , якщо для будь-якого справедлива тотожність

.

Приклад 1. Рівняння є однорідним, бо

.

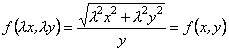Однорідні диференціальні рівняння першого порядку зводяться до рівнянь з відокремлюваними змінними за допомогою підстановки Тоді (тут покладено ). Змінні відокремлюються, оскільки після підстановки в рівняння дістанемо

,

звідки

.

Інтегруючи це рівняння й повертаючись від змінної до змінної , отримуємо загальний розв’язок однорідного рівняння.

Прикладі 2. Розв’язати рівняння .

Р о з в ‘ я з о к. Це рівняння однорідне. Виконаємо у цьому рівнянні заміну залежної змінної Тоді

.

Відокремлюючи змінні, одержуємо: , звідки

.

Отже, загальний розв’язок рівняння має вигляд .

Приклад 3. Покажемо, як розв’язується рівняння, наведене в прикладі 3, за допомогою полярних координат.

Перейдемо до нових змінних та за формулами

.

Звідси

Отже,

.

Права частина рівняння у нових координатах набуває вигляду

Прирівнюючи праву і ліву частини рівняння, дістанемо

.

На основі властивості пропорції позбудемося дробів:

Спрощуючи це рівняння, отримаємо

.

Відокремлюємо змінні

.

Інтегруємо

.

(довільну сталу позначили як ) . Звідси .

Повернемось до старих змінних та й спростимо вираз. Отримаємо шуканий загальний інтеграл