Сторінка
6

Квадратичні форми, їх приведення до діагонального (канонічного) вигляду

Перший критерій продуктивності. Матриця продуктивна тоді і тільки тоді, коли матриця існує і її елементи невід’ємні.

Другий критерій продуктивності. Матриця з невід’ємними елементами продуктивна, якщо сума елементів за довільним її стовпцем (рядком) не перевищує одиниці:

(4.40)

причому хоча б для одного стовпця (рядка) ця сума строго менша одиниці.

Приклад. 1. Дані балансу трьох галузей промисловості за деякий період записані в табл.1. Потрібно знайти об’єм валового випуску продукції, якщо кінцеве споживання за галузями збільшити відповідно до 60, 70 і 30.

Таблиця 1

Р о з в ‘я з о к. Випишемо вектори валового випуску і кінцевого споживання та матрицю коефіцієнтів прямих затрат. Згідно формул (4.36) і (4.38),

Матриця задовольняє обидва критерії продуктивності. У випадку заданого збільшення кінцевого споживання новий вектор кінцевого продукту буде мати вигляд .

Потрібно знайти новий вектор валового випуску , що задовольняє співвідношенням балансу в припущенні, що матриця не зміниться. В такому випадку компоненти невідомого вектора знаходяться із системи рівнянь, яка в матричній формі має вигляд (4.37) або де матриця має вигляд

Звідси розраховується новий вектор як розв’язок рівняння

Знайдемо обернену матрицю (матрицю повних затрат ) (обчислення проводимо з точністю до третього знаку):

.

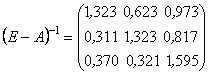Зауважимо, що знайдена обернена матриця задовольняє першому критерію продуктивності матриці

Тепер вичислюємо вектор валового випуску

Таким чином, для того щоби забезпечити задане збільшення компонент вектора кінцевого продукту, необхідно збільшити відповідні валові випуски: добування і переробку вуглеводів на 52,2%, рівень енергетики – на 35,8% і випуск машинобудування – на 85% в порівнянні з початковими величинами, що приведені в табл.1.

4.5.2. Лінійна модель торгівлі

Процес взаємних закупок товарів аналізується з

використанням понять власного числа і власного вектора матриці. Припустимо, що бюджети країн витрачаються на покупку товарів. Розглянемо лінійну модель обміну, або модель міжнародної торгівлі.

Нехай доля бюджету яку а країна витрачає на закупку товарів у ої країни. Введемо матрицю коефіцієнтів

. (4.41)