Сторінка
4

Квадратичні форми, їх приведення до діагонального (канонічного) вигляду

Приклад 2. Визначити, яку криву визначає рівняння

і побудувати її.

Р о з в ’ я з о к. Характеристичне рівняння має вигляд

Розв’язавши це рівняння, одержимо . Знайдемо тепер власні вектори. Якщо , маємо таку систему рівнянь для знаходження власного вектора :

Звідси знаходимо .

При маємо систему рівнянь

.

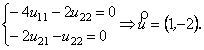Зводимо власні вектори і до одиничних:

.

Отже, перетворення координат записується так:

.

Лінійна частина рівняння набуває вигляду

Задане рівняння стає таким:

Якщо здійснити в цьому рівнянні паралельне перенесення системи координат за формулами , то, прирівнявши до нуля коефіцієнти при і і розв’язавши відповідну систему рівнянь одержимо

Рівняння відносно і набирає найпростішої (канонічної ) форми:

еліпс.

Отже, дане рівняння є еліпсом (рис. 4.1).

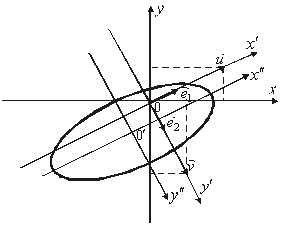
Рис. 4.1

Приклад 3. Визначити, яку поверхню визначає рівняння

.

Р о з в ’ я з о к. Характеристичне рівняння має вигляд

.

Коренями цього рівняння є .

Власні вектори:

для

для

Третій власний вектор знайдемо з умови

Одиничні вектори:

Перетворення координат:

Підставивши ці формули в лінійну частину рівняння поверхні другого порядку, одержимо

У нових координатах рівняння буде таким:

Паралельне перенесення за формулами приведе до рівняння

(однопорожнинний гіперболоїд).

Паралельно з цим було знайдено і координати початку координатної системи по відношенню до системи координат :

4.5. Застосування елементів лінійної алгебри в економіці

Для розв’язування багатьох економічних задач використовуються елементи алгебри матриць, теорії систем лінійних алгебраїчних рівнянь. Особливо при розробці і використання баз даних: при роботі з ними майже вся інформація зберігається і обробляється в матричній формі.

4.5.1. Модель Леонт’єва багатогалузевої економіки

Макроекономіка функціонування багатогалузевого господарства вимагає балансу між окремими галузями. Кожна галузь, з одного боку, є виробником, а з іншого – споживачем продукції, що випускається іншими галузями. Виникає досить непроста задача розрахунку зв’язку між галузями через випуск і споживання продукції різного виду. Вперше ця проблема була сформульована у вигляді математичної моделі в працях відомого американського економіста В.Леонт’єва в 1936 р., який спробував проаналізувати причини економічної депресії США 1929-1932 рр. Ця модель основана на алгебрі матриць і використовує апарат матричного аналізу.

Для простоти будемо вважати, що виробнича сфера господарства представляє собою галузей, кожна з яких виробляє свій однорідний продукт. Для забезпечення виробництва кожна галузь потребує продукцію інших галузей. Процес виробництва розглядається за деякий період, наприклад, за рік.

Введемо позначення:

загальний об’єм продукції ої галузі (її валовий випуск);

об’єм продукції ої галузі, що споживається ою галуззю при виробництві об’єму продукції ;

об’єм продукції ої галузі, що призначена для реалізації (споживання) в невиробничій сфері, або так званий продукт кінцевого споживання. До нього відносяться особисте споживання громадян, задоволення суспільних потреб, утримання державних інститутів і т.д.