Сторінка
2

Метод розкладу визначника в суму визначників

Di =(-1)i+i×x×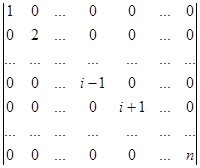= (-1)2i×x×1×2×…×(i-1)×(i+1)×…×n =

=×x×1×2×…×(i-1)×(i+1)×…×n =×n!.

Таким чином,

D1 = ×n! = x×n!; D2 = ×n!; D3 = ×n!; .; Dn = ×n!.

Остаточно,

D= D0+D1+D2+D3+ .+Dn = n! + x ×n! + ×n! + ×n! + .+ ×n! =

= n!().

Приклад 17. Обчислити визначник

D=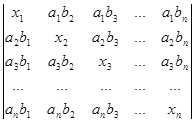

Розв’язування. Зрозуміло, що порядок визначника дорівнює n (наприклад, на головної діагоналі n елементів). Діагональні елементи визначника можна подати у вигляді

xi = xi-aibi + aibi; i = 1,2,…,n.

Тобто

D= .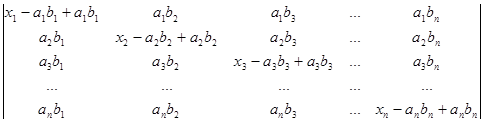

Розкладемо перший рядок визначника в сумі двох рядків:

(x1,a1b2, a1b3,…, a1bn) = (x1-a1b1+ a1b1,a1b2, a1b3,…, a1bn) =

= (a1b1,a1b2, a1b3,…, a1bn) + (x1-a1b1,0, 0,…, 0).

Аналогічно, в суму двох рядків розкладемо решту рядків:

(a2b1, x2,a2b3,…, a2bn) = (a2b1,x2-a2b2+ a2b2, a2b3,…, a2bn) =

= (a2b1,a2b2, a2b3,…, a2bn) + (0,x2-a2b2,0,…, 0).

(a3b1, a3b2, x3,…, a3bn) = (a3b1,a3b2, x3-a3b3+ a3b3, …, a3bn) =

= (a3b1,a3b2, a3b3,…, a3bn) + (0,0,x3-a3b3,…, 0).

(anb1, anb2, anb3,…, xn) = (anb1,anb2,anb3, …, xn-anbn+ anbn) =

= (anb1,anb2, anb3,…, anbn) + (0,0,0,…, xn-anbn).

За першим рядком визначник D розкладемо в суму двох визначників:

D= .+

+ .

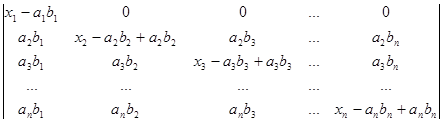Далі кожен з одержаних визначників розкладемо в суму двох визначників за другим рядком. Одержуємо суму чотирьох визначників:

D= .+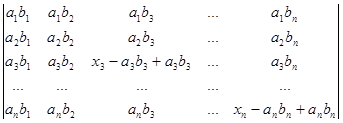

+ +

+ +

+.

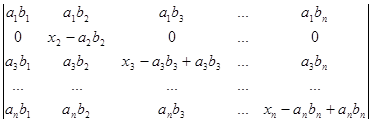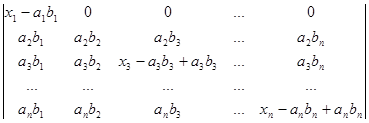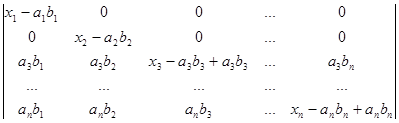Кожний з одержаних визначників можна розкласти в суму двох визначників за 3-м рядком і т.д. На кожному кроці число доданків збільшується в два рази. Після розкладу в суму послідовно за всіма рядками одержуємо суму 2n визначників.

Рядки, в суму яких розкладається даний рядок початкового визначника, поділимо на два типи. Рядками першого типу будемо вважати рядки (a1b1,a1b2, a1b3,…, a1bn), (a2b1,a2b2, a2b3,…, a2bn), (a3b1, a3b2, a3b3,…, a3bn), ., (anb1,anb2, anb3,…, anbn). Рядки другого типу – це рядки (x1-a1b1,0, 0,…, 0), (0,x2-a2b2,0,…, 0), (0,0,x3-a3b3,…, 0), ., (0,0,0,…, xn-anbn). Після розкладу визначника в суму послідовно за всіма рядками одержуємо суму визначників, які мають лише рядки першого та другого типів. Неважко переконатись в тому, що рядки першого типу пропорційні. Тому визначник, який має принаймні два рядки першого типу, дорівнює нулю. Для того, щоб знайти величину визначника D, достатньо взяти лишу суму ненульових визначників. У кожному з таких визначників не більше одного рядка першого типу. Якщо визначник не має рядків першого типу, то всі його рядки другого типу і визначник має вигляд

D0= .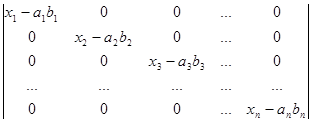

Якщо у визначнику єдиний рядок першого типу, то решта рядків є рядками другого типу. Рядок першого типу у такому визначнику може бути на першому місці, на другому і т.д. Тому існує n таких визначників:

D1= ,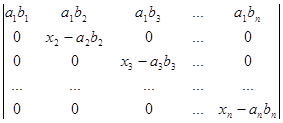

D2= ,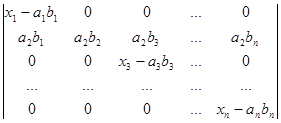

D3= ,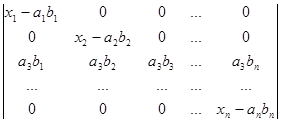

Dn= .

Таким чином,

D= D0+D1+D2+D3+ .+Dn.

Визначник D0 є визначником трикутного вигляду відносно головної діагоналі. Тому

D0= 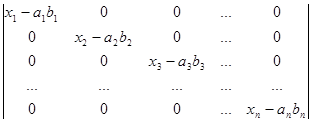= (x1-a1b1)(x2-a2b2)(x3-a3b3)… (xn-anbn).

Обчислимо визначник Di при і ³ 1.

Dі = .

Розкладемо визначник Dі на за елементами і-го стовпчика:

Dі = (-1)і+iaіbі =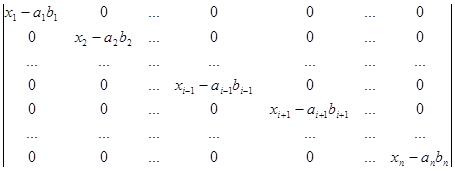

= (-1)2і aіbі (x1-a1b1)(x2-a2b2)(x3-a3b3) .(xі-1-aі-1bі-1) (xі+1-aі+1bі+1)…(xn-anbn) =

= aіbі (x1-a1b1)(x2-a2b2)(x3-a3b3) .(xі-1-aі-1bі-1) (xі+1-aі+1bі+1)…(xn-anbn).

Одержуємо

D= D0+D1+D2+D3+ .+Dn = (x1-a1b1)(x2-a2b2)(x3-a3b3)… (xn-anbn) +

+ a1b1 (x2-a2b2)(x3-a3b3) .(xn-anbn) + a2b2 (x1-a1b1)(x3-a3b3) .(xn-anbn) +

+ a3b3 (x1-a1b1)(x2-a2b2)(x4-a4b4) .(xn-anbn) + .+ anbn (x1-a1b1)(x2-a2b2)(x3-a3b3)…(xn-1-an-1bn-1) = = (x1-a1b1)(x2-a2b2)(x3-a3b3)…(xn-anbn) .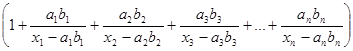

Приклад 18. Обчислити визначник

D= .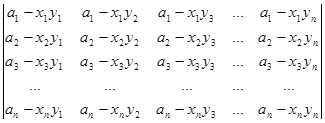

Розв’язування. Зрозуміло, що порядок визначника дорівнює n. Розкладемо кожний рядок визначника в суму двох рядків:

(a1-x1y1, a1-x1y2, a1-x1y3,…,a1-x1yn) = (a1, a1, a1,…,a1) + (-x1y1,-x1y2,-x1y3,…,-x1yn)

(a2-x2y1, a2-x2y2, a2-x2y3,…,a2-x2yn) = (a2, a2, a2,…,a2) + (-x2y1,-x2y2,-x2y3,…,-x2yn)

(a3-x3y1, a3-x3y2, a3-x3y3,…,a3-x3yn) = (a3, a3, a3,…,a3) + (-x3y1,-x3y2,-x3y3,…,-x3yn)

………………………………………………………………………………………

(an-xny1, an-xny2, an-xny3,…,an-xnyn) = (an, an, an,…,an) + (-xny1,-xny2,-xny3,…,-xnyn).

Розкладемо визначник в суму двох визначників за другим рядком:

D= +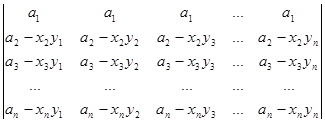

+ .

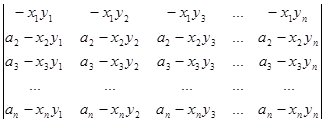Далі кожен з двох одержаних визначників можна розкласти в суму двох визначників за другим рядком. Одержуємо суму чотирьох визначників:

D= +

+ +

+ +

+ .

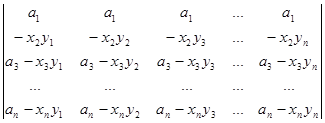Кожний з одержаних визначників можна розкласти в суму двох визначників за 3-м рядком і т.д. Після розкладу в суму послідовно за всіма рядками одержуємо 2n визначників.