Сторінка
3

Метод розкладу визначника в суму визначників

Рядки, в суму яких розкладаються рядки початкового визначника, умовно поділимо на два типи. Рядками першого типу будемо вважати рядки (a1, a1, a1,…,a1), (a2, a2, a2,…,a2), (a3, a3, a3,…,a3), ., (an, an, an,…,an). Рядками другого типу будемо вважати рядки (-x1y1,-x1y2, -x1y3,…,-x1yn), (-x2y1,-x2y2,-x2y3,…,-x2yn), (-x3y1,-x3y2,-x3y3,…,-x3yn), .,(-xny1,-xny2,-xny3,…,-xnyn). Після розкладу визначника в суму 2n визначників кожен з цих визначників складається з рядків або першого, або другого типу. Але два рядки першого типу пропорційні, також пропорційні два рядки другого типу. При n³3 кожен з одержаних визначників має принаймні два рядки одного типу, тобто пропорційні рядки. Це означає, що при n³3 кожен з 2n визначників, в суму яких розкладається початковий визначник, дорівнює нулю, а тому D=0.

Залишається розглянути випадки n = 1, n = 2.

При n = 1 D= a1-x1y1.

При n = 2 розкладемо визначник в суму двох визначників за першим рядком

D = = + .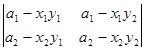

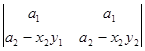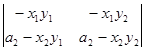Кожен з одержаних визначників розкладемо в суму двох визначників за другим рядком. Одержуємо суму чотирьох визначників.

D = + + + .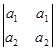

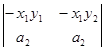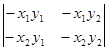Серед одержаних чотирьох визначників перший і останній дорівнюють нулю, оскільки мають пропорційні рядки, тому

D = + .

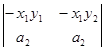Виносимо множники з рядків визначників:

D = -a1x2 ‑ x1a2= -a1x2 (y2-y1) -x1a2 (y1-y2) =

= a1x2 (y1-y2) -x1a2 (y1-y2) = (y1-y2) (a1x2 -x1a2).

Задачі для самостійного розв’язування.

Обчислити визначники методом розкладу в суму.

1.

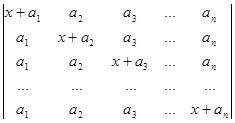
2.

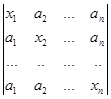
3.

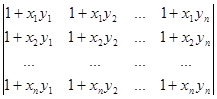
4.

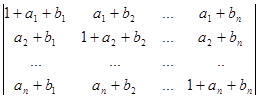
5.

6.

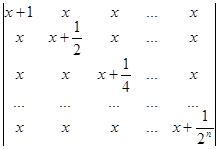
7.

Список літератури

1. Курош А.Г. Курс высшей алгебры. – М., 1965.

2. Проскуряков И.В. Сборник задач по линейной алгебре. – М., 1984.

3. Фаддеев Д.К., Соминский И.С. Сборник задач по высшей алгебре. – М., 1977.