Сторінка
3

Основні означення та факти з теорії визначників

Аналогічно, якщо і-й рядок визначника D є сумою k рядків, то визначник D можна розкласти в суму k визначників за і-м рядком.

7. Якщо до рядка визначника додати інший рядок, помножений на число, то визначник не змінюється.

Нехай ,, .,‑ деякі рядки визначника D, а l1,l2, .,ln – деякі числа. Тоді рядок l1+l2+ .+lnназивається лінійною комбінацією рядків ,, .,

8. Якщо у визначнику деякий рядок є лінійною комбінацією інших рядків, то визначник дорівнює нулю.

9. Якщо до рядка визначника додати лінійну комбінацію інших рядків, то визначник не змінюється.

Теорема про розклад визначника за елементами рядка (стовпчика).

Нехай

D = .

Доповнюючим мінором Mij елемента aij називається визначник порядку n-1, який одержується з визначника D викресленням і-го рядка і j-го стовпчика. Тобто викреслюються рядок та стовпчик, в яких знаходиться елемент aij.

Алгебраїчним доповненням елемента aij називається число

Aij=(-1)і+jMіj

Теорема.

Визначник n–го порядку дорівнює сумі добутків елементів будь-якого фіксованого рядка на їх алгебраїчні доповнення.

Наприклад, розкладемо визначник D за елементами і-го рядка

D = ai1Ai1+ai2Ai2+…+ainAin.

Розкладемо визначник

D =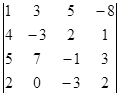

за елементами 3-го рядка.

D = 5×(-1)3+1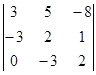+ 7×(-1)3+2 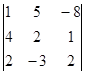+ (-1) ×(-1)3+3+

+3×(-1)3+4=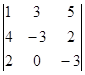

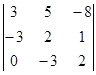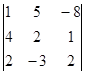= 5‑ 7‑ ‑ 3.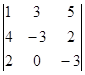

Наслідок 1. Визначник n–го порядку дорівнює сумі добутків елементів будь-якого фіксованого стовпчика на їх алгебраїчні доповнення.

Наслідок 2. Сума добутків елементів рядка (стовпчика) визначника на алгебраїчні доповнення іншого рядка (стовпчика) дорівнює нулю.

Визначник Вандермонда.

Визначником Вандермонда n–го порядку називається визначник

Dn = .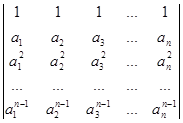

Визначник Вандермонда дорівнює

Dn = (a2-a1)(a3-a1)(a3-a2)×…×(an-a1)(an-a2)×…×(an-an-1) = .