Сторінка
2
A =  .
.
Визначником n–го порядку матриці A називається алгебраїчна сума всіх можливих добутків її елементів, побудованих за правилом: з кожного рядка і з кожного стовпчика матриці береться по одному і лише по одному елементу. Якщо після упорядкування співмножників у добутку за другим індексом перші індекси утворюють парну перестановку, перед добутком ставиться знак +, якщо непарну перестановку, то перед добутком ставиться знак ‑.
Таким чином, на відміну від першого означення визначника, за другим означенням знак при добутку визначається парністю перестановки перших індексів при упорядкуванні співмножників за другим індексом.
Теорема..
Два означення визначника еквівалентні.
Користуючись другим означенням визначник D матриці A можна записати аналітично так:
D = ![]()
![]() ,
,
де сума береться по всім перестановкам чисел 1,2, .,n. ![]()
Визначники трикутного вигляду.
Нехай
D = 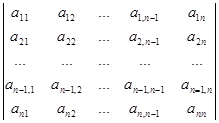 .
.
У визначнику D можна визначити дві діагоналі. Головну діагональ утворюють елементи a11,a22,…,an-1,n-1,ann; побічну діагональ утворюють елементи a1n,a2,n-1,…,
an-1,2,an1.
Визначником трикутного вигляду відносно головної діагоналі називається визначник, всі елементи якого, що знаходяться вище або нижче головної діагоналі, дорівнюють нулю.
Наприклад,
D = 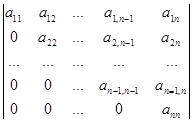 .
.
Визначник трикутного вигляду відносно головної діагоналі дорівнює добутку елементів головної діагоналі
D = 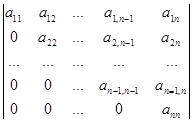 = a11a22…an-1,n-1ann.
= a11a22…an-1,n-1ann.
Визначником трикутного вигляду відносно побічної діагоналі називається визначник, всі елементи якого, що знаходяться вище або нижче побічної діагоналі, дорівнюють нулю.
D1 = 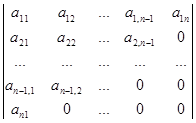 .
.
Визначник трикутного вигляду відносно побічної діагоналі дорівнює добутку елементів побічної діагоналі зі знаком ![]() , де n – порядок визначника.
, де n – порядок визначника.
D1 = 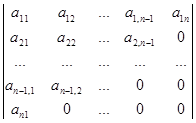 =
=![]() a1na2,n-1…an-1,2an1.
a1na2,n-1…an-1,2an1.
Транспонування матриці.
Нехай дана матриця A порядку m x n
A =  .
.
Складемо нову матрицю B за такими правилами. Запишемо елементи першого рядка матриці A, зберігаючи їх порядок, до першого стовпчика матриці B. Далі елементи другого рядка матриці A, зберігаючи їх порядок, запишемо до другого стовпчика матриці B і т.д. Такий процес називається транспонуванням матриці A. В результаті одержимо матрицю B порядку n x m, яка називається транспонованою матрицею для матриці A і позначається AT.
AT = 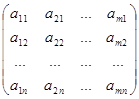 .
.
Зрозуміло, що (AT)T = A.
Теорема..
Нехай A – квадратна матриця. Тоді визначники матриць AT і A рівні.
Таким чином, транспонування не змінює визначника матриці. Далі будемо вважати визначники взаємно транспонованих матриць тотожними.
Властивості визначників.
Зауваження. Будемо формулювати властивості визначників для рядків визначників. Але при цьому будемо враховувати, що вони вірні і для стовпчиків визначників.
1. Якщо всі елементи деякого рядка визначника дорівнюють нулю (нульовий рядок), то визначник дорівнює нулю.
2. Якщо у визначнику переставляються місцями два рядки, то змінюється лише знак визначника.
Припустимо, що у визначнику D міняються місцями і-й і j-й рядки (і¹j), тоді
D = 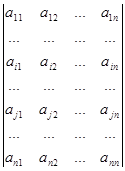 = -
= - 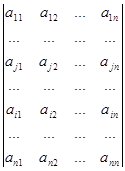 .
.
3. Якщо два рядки визначника співпадають, то визначник дорівнює нулю.
4. Якщо деякий рядок визначника помножується на число l, то визначник помножується на l.
Припустимо, що у визначнику
D =
помножується на l і-й рядок, тоді
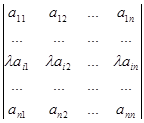 = l
= l = lD.
= lD.
З цієї властивості випливає, що якщо всі елементи деякого рядка визначника помножені на деяке число l, то це число можна винести за знак визначника як множник.
Два рядки визначника називаються пропорційними, якщо один з них можна одержати помноженням другого на деяке число.
5. Якщо два рядки визначника пропорційні, то визначник дорівнює нулю.
Нехай (bi1, bi2,…,bin) і (сi1, сi2,…,сin) – два рядки. Під сумою цих рядків розуміється рядок вигляду (bi1+сi1, bi2 +сi2,…,bin+сin).
6. Якщо у визначнику D і-рядок є сумою двох рядків, то визначник D можна розкласти в суму двох визначників D1 і D2 за і-м рядком таким чином, що і-рядком визначника D1 є перший доданок, а і-м рядком визначника D2 – другий доданок і-го рядка визначника D. Решта рядків визначників D1 і D2 співпадають з відповідними рядками визначника D.
Припустимо, що у визначнику D і-й рядок є сумою двох рядків, тоді
D =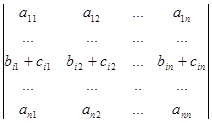 =
= 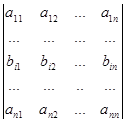 +
+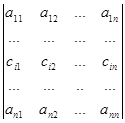 .
.
Інші реферати на тему «Математика»:
Лінійні неоднорідні системи
Поняття множини. Змінні та постійні величини
Побудова множинних фільтрів для лінійних алгебраїчних систем
Неперервність функції в точці і в області.Дії над неперервними функціями
Застосування подвійних інтегралів до геометричних і фізичних задач. Обчислення інтеграла Пуассона
