Сторінка
6

Джерела статистики, види середніх та способи їх обчислення

Перевіримо передумови:

Vx = 7,488%; Vy = 8,336%.

Варіація недостатня по ряду Х, і недостатня по ряду У.

2. gхmin = 1,818 < 3; gхmax = 1,524 < 3;

gymin = 2,035 < 3; gymax = 1,225 < 3.

Сукупність 25 підприємств є однорідною, як за ознакою Х так і за ознакою У. Для того щоб обґрунтувати вибір математичного рівняння побудуємо кореляційне поле. Прямолінійну форму зв’язку визначають рівнянням прямої лінії: yx =a0+a1x,

na0 + a1åxi = åyi

a0åxi + a1åxi2 = åxiyi

25a0 + 1997a1 = 993,5

1997a0 + 160415a1 = 79582,80

D = 22366; Da0 = 445450,9; Da1 = 5550,5, звідси знаходимо коефіцієнти регресії: a0 = 19,91643, a1 = 0,248167.

Отже, рівняння кореляційного зв’язку між прибутком і обсягом виробництва матиме такий вигляд:

yx = 19,91643 + 0,248167×х

В досліджуваній сукупності товариств із збільшенням обсягу виробництва на 1 тис. т. прибуток збільшується в середньому на 0,248 тис. грн. Параметр a0 як вільний член рівняння має тільки розрахункове значення.

Визначимо міру впливу фактора на результат. Для оцінки міри впливу фактора на результат обчислюють індекс кореляції який обчислюється як відношення двох дисперсій:

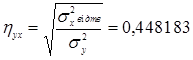
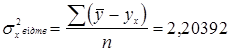
Також ще можна обчислювати коефіцієнт кореляції:

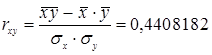
Коефіцієнт кореляції показує, що між обсягом виробництва і прибутком у досліджуваних підприємствах зв’язок прямий і слабкий.

h2 = Д = 20,08 %

Прибуток на 20,08% пояснюється впливом обсягом виробництва, і на 79,92% впливом неврахованих факторів.

Суттєвість коефіцієнта детермінації будемо перевіряти, використовуючи критерій Фішера.

Н0: Обсяг виробництва не впливає суттєво на прибуток.

F0,95(1;23) = 4,28; Fh2 = 5,781216

Fh2 < F0,95 Отже гіпотеза Н0 не відхиляється. Залежність між фактором і результатом є несуттєвою.

Ми дослідили вплив обсягу виробництва на прибуток і можемо зробити висновок – обсяг виробництва на прибуток майже не впливає.

Кореляція, за допомогою якої вивчається вплив на величину результативної ознаки двох і більше факторних ознак, називається множинною. Показники щільності зв’язку при множинній кореляції є парні, часткові і множинні (сукупні) коефіцієнти кореляції і множинний коефіцієнт детермінації.

Парні коефіцієнти кореляції використовують для вимірювання щільності зв’язку між двома досліджуваними ознаками без урахування їх взаємодії з іншими ознаками.

Часткові коефіцієнти кореляції характеризують щільність зв’язку результативної ознаки з однією факторною ознакою при умові, що інші факторні ознаки перебувають на постійному рівні.

Коефіцієнт множинної (сукупної) детермінації показує, яка частка варіації досліджуваного результативного показника зумовлена впливом факторів, включених у рівняння множинної регресії.

Основним показником щільності зв’язку при множинній кореляції є коефіцієнт множинної кореляції. Він повинен бути найбільшим серед всіх інших коефіцієнтів множинної кореляції.

Таблиця 3.3

Вихідні та розрахункові дані для обчислення множинної кореляції