Сторінка
3

Джерела статистики, види середніх та способи їх обчислення

Середні величини в статистиці належать до класу степеневих середніх, які описує формула

,

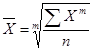де X — рівень ознаки, варіант; п — число варіантів; т — показник степеня середньої.

Зміна степеня середньої величини визначає її вигляд:

- т = 1 - середня арифметична;

- т = 0 - середня геометрична;

- т = -1- середня гармонійна;

- т = 2 - середня квадратична;

- т = 3 - середня кубічна.

Їхні відповідні формули мають такий вигляд:

- (середня арифметична);

- (середня геометрична);

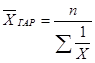- (середня гармонійна);

- (середня квадратична);

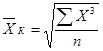- (середня кубічна).

Із степеневих середніх у статистиці найчастіше використовують середню арифметичну, рідше — середню гармонійну, середню гео­метричну — тільки для обчислення середніх темпів динаміки, а середню квадратичну — для розрахунків показників варіації. Серед­ню кубічну майже не використовують. Вирішити, яку саме середню потрібно застосовувати в окремому випадку, можна шляхом аналізу конкретної досліджуваної сукупності. Вірну характеристику сукуп­ності за варіаційною ознакою в кожному окремому випадку дає тільки певний вид середньої.

Крім степеневих середніх, у статистиці використовують описові характеристики розподілу варіаційної ознаки — моду і медіану, які характеризують структуру сукупності, тому їх іще називають струк­турними середніми.

Добір середніх має ґрунтуватися на позиціях діалектичного ро­зуміння категорій загального та індивідуального, масового та оди­ничного. У кожному випадку слід пам'ятати про вимоги стосов­но середніх, що треба знайти.

- Визначення середньої на підставі масових даних. Індивідуальні значення досліджуваної ознаки в окремих одиниць сукупності мають бути різними. Для того щоб дістати науково обґрунтовану типову величину, обчислювати середню слід за даними, до яких залучається якнайбільше одиниць цієї сукупності. В разі уза­гальнення масових фактів випадкові відхилення індивідуальних величин від загальної тенденції взаємно погашаються в середній величині. Ця вимога в статистиці пов'язує середні величини із законом великих чисел.

- Якісна однорідність, одноманітність сукупності, для якої визна­чають середню. Це означає, що не можна застосовувати середні до таких сукупностей, окремі частини яких підлягають різним законам розвитку відносно осереднюваної ознаки. Якщо, наприклад, визначити середню врожайність сільськогос­подарських культур, то не можна її розраховувати, склавши разом урожай зернових і технічних культур. Така середня не відображує особливостей цього явища і є не науковою, а фіктивною. Саме тому застосування методу середніх пов'язують з методом групування. Потрібно будь-яку досліджувану сукупність розчленувати спочатку на однорідні групи за певною ознакою, а вже потім визначати середню досліджуваної ознаки.

2.2. Середня арифметична проста і зважена

Одним з найпоширеніших видів середньої є середня арифме­тична, її застосовують в тих випадках, коли обсяг варіаційної ознаки для всієї сукупності формується як сума значень ознаки в окремих одиниць досліджуваної сукупності. Для того щоб розрахувати серед­ню арифметичну, потрібно скласти всі окремі варіанти (індивідуальні значення ознаки) і суму поділити на їхню кількість.

Наприклад, відомо, що тарифний розряд робітників бригади, яка складається з восьми чоловік, становить: 3, 4, 3, 5, 4, 5, 4, 4. Треба знайти середній рівень кваліфікації робітників бригади. Для цього скла­демо тарифний розряд кожного робітника і добуту суму поділимо на кількість робітників:

.

Позначивши варіанти X1, Х2 тощо, визначимо середню арифме­тичну за такою формулою:

.

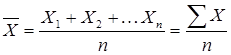Середня арифметична буває двох видів - проста і зважена. Наведена вище середня є середньою арифметичною простою і визна­чають її двома простими операціями - складанням значень варіантів і діленням отриманої суми на їхню кількість.

Проте такий розрахунок середньої можна дещо спростити: перед додаванням помножити варіанти на частоти, тобто на число, що вказує на те, скільки разів цей варіант трапляється у відповідному ряді.

Таке множення варіантів на їхні частоти в статистиці називають зважуванням, а обчислена в такий спосіб середня - середньою арифметичною зваженою.

Обчислення середньої зваженої в цьому прикладі має такий вигляд:

.

Якщо частоту (вагу) позначити f, то формула середньої арифме­тичної зваженої має такий вигляд:

.

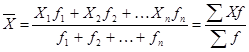У наведеному прикладі за цією формулою обчислювати середню набагато легше, ніж за формулою простої арифметичної. Отже, для визначення середньої арифметичної зваженої виконують такі опе­рації: множення кожного варіанта на його частоту, підсумовування отриманих добутків і, врешті, ділення добутої суми на суму частот.

Переважно середню арифметичну визначають за формулою се­редньої зваженої. Просту середню використовують тільки у випадках, коли в кожного варіанта частота дорівнює одиниці, тобто варіант трапляється один раз. Якщо частоти всіх варіантів однакові, то при Визначенні середньої арифметичної можна також відмовитися від зважування.