Сторінка
2

Інтегрування з допомогою заміни змінної та інтегрування частинами

Зауваження. Якщо в цьому твердженні відкинути умову , то воно може виявитись хибним. Нехай, наприклад, дано інтеграл Первісною тут є - обмежена функція , але подвійна підстановка не має змісту, бо при не прямує ні до якої границі: інтеграл не існує.

20. Інтеграл тоді й тільки тоді збіжний, коли будь-якому заданому числу відповідає таке число , що при і виконується нерівність

Приклад. Довести, що 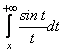- збіжний.

Д о в е д е н н я.

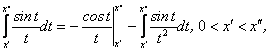
звідси 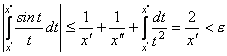, якщо тобто

30. Якщо збіжний, то збіжним є також інтеграл і при цьому . Інтеграл називається абсолютно збіжним, якщо 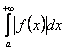збіжний.

40. Теорема порівняння. Якщо для виконується нерівність , причому ці обидві функції невід’ємні, то із збіжності інтеграла 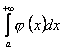випливає збіжність інтеграла , а із розбіжності випливає розбіжність .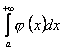

Як функція порівняння, важливу роль відіграє функція . Оскільки і , одразу ж стає зрозумілим, що збіжний при і розбіжний, якщо

Приклади. Дослідити збіжність інтегралів:

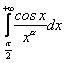а), б) , в)

Р о з в ’ я з о к. а) Оскільки , то

Безпосереднім обчисленням останнього інтеграла легко встановити, що він збіжний при Тому і даний інтеграл є збіжний при Неважко довести, що при інтеграл розбіжний.

б) Інтегруванням частинами дістанемо

Звідси елементарно одержимо такі висновки: заданий інтеграл збіжний при ; якщо , то збіжність буде неабсолютною; при інтеграл збіжний абсолютно, бо

при інтеграл розбіжний.

в) Для дослідження інтеграла доведемо спочатку, що існує таке , за якого вірна нерівність Оскільки при ця нерівність виконується, то для тих значень , за яких , виконуватиметься і дана нерівність.

Нерівність для похідних лівої і правої частин набирає вигляду і виконується при . Справді, маємо , що істинно. Отже, для всіх маємо . Інтеграл збіжний, якщо збіжним є інтеграл . Оскільки для то 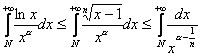збіжний при , тобто при для всіх скінчених .