Сторінка
3

Інтегрування з допомогою заміни змінної та інтегрування частинами

Цілком очевидно, що при заданий інтеграл розбіжний.

На основі теореми порівняння створено ряд конкретних критеріїв збіжності невласних інтегралів. Заслуговує на увагу і такий критерій збіжності:

50. Якщо існує границя

,

то із збіжності інтеграла 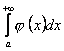при випливає збіжність інтеграла , а із розбіжності першого інтеграла при C > 0 випливає розбіжність другого.

Сформулюємо ще одну ознаку збіжності, незалежну від теореми порівняння і застосовну навіть для знакозмінної підінтегральної функції.

60. Якщо інтеграл є обмеженою функцією величини , тобто , а -

монотонна функція, що прямує до нуля при , то інтеграл

збіжний.

З цим, а також з іншими критеріями збіжності інтегралів детальніше можна ознайомитись в кн. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. – Т. 3. – М., Л.: Гостехиздат, 1949.

9.7.2. Невласні інтеграли від необмежених функцій

Нехай на інтервалі задана функція , яка хоча б на одному із кінців або навіть всередині інтервалу має розриви другого роду, наприклад, при

Розглянемо інтеграл 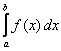. Виникає питання про те, існує чи ні такий інтеграл. Якщо існує, то за яких умов і як його обчислювати. Розглянемо наприклад, інтеграл

У цьому інтегралі в точках підінтегральна функція перетворюється в нескінченність ( розриви другого роду ) . Природно, границі інтегрування за обчислень замінити на , щоб виключити з розгляду точки розриву. В результаті одержимо

Якщо тепер перейти до границі при , то одержимо

Повертаючись до загальних міркувань, формально можна записати, вважаючи, що у всіх вказаних точках функція має розриви другого роду:

Кожний з інтегралів праворуч можна записати як суму двох інтегралів, вибравши між точками ще одну точку Тоді

Тобто завжди можна кожний з інтегралів звести до такого вигляду, щоб підінтегральна функція мала розрив лише на одному з кінців інтервалу інтегрування.

Отже, далі підлягають детальному вивченню інтеграли від розривних функцій лише в тому випадку, коли тільки на одній з границь інтегрування функція має розрив.

Означення.Якщо для інтеграла при , де або не існує, або дорівнює , існує скінчена границя, то його називають невласним інтегралом функції від до і позначають

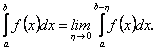
За цієї умови інтеграл називають збіжним, а функцію інтегрованою на інтервалі . Якщо ж ця границя нескінченна або не існує, то його називають розбіжним. У тому випадку, коли підінтегральна функція має розрив за значення, що дорівнює нижній границі інтегрування , інтеграл можна звести до того випадку, коли розрив відповідатиме верхній границі інтегрування:

де функція має розрив у точці , або

Приклади. 1)

У цьому інтегралі підінтегральна функція розривна при , якщо . Маємо

Відповідно до визначення заданий інтеграл збіжний, якщо і розбіжний, якщо

2)

Підінтегральна функція тут має розриви на обох кінцях інтегрування при i . Тому інтеграл запишемо так:

Тут у першому інтегралі розрив при , а в другому при .