Сторінка
8

Поняття множини. Змінні та постійні величини

Одержана функція від функції називається складною функцією змінної . Функція - внутрішня, а функція - зовнішня. Наприклад:

Розглянемо функції багатьох змінних. Тут ми маємо два напрямки.

1. Нехай - функція багатьох змінних , кожна з яких є функцією незалежної змінної : . Тоді функція

складна функція незалежної змінної .

Наприклад:

є складна функція незалежної змінної .

2. Нехай - функція багатьох змінних , аргументи якої, в свою чергу, залежать від двох або більшого числа змінних:

.

Тоді функція

буде складною функцією незалежних змінних .

Наприклад: .

5.3.3. Поняття оберненої функції

Нехай функція визначена в деякій області . Візьмемо будь-яке значення

Нехай функція визначена в деякій області . Візьмемо будь-яке значення із множини значень цієї функції . В області означення функції знайдеться одне або декілька значень аргументу таких, що . Поставимо у відповідність всі ці значення . При цьому кожному значенню змінної ставиться у відповідність одне або декілька значень . А це означає, що на множині задається однозначна або багатозначна функція . Вона називається оберненою до функції . Областю. визначення оберненої функції є область зміни даної функції.

Приклади.

1.

Функція є однозначною оберненою функцією для функції (рис.5.15).

:

2. :

таких, що . Тому функція :

обернена для функції , буде двозначною (рис.5.16).

Рис.5.15 Рис.5.16

Розглянемо питання про графік оберненої функції. Функція та її обернена функція виражають один і той самий зв’язок між змінними і , лише у першому випадку розглядаємо як аргумент, - як функцію, а в другому випадку – навпаки. Тому графік оберненої функції співпадає з графіком функції (рис.5.17).

Якщо в оберненої функції, як і в заданій, аргумент позначити через , а значення функції - через , то вона запишеться так: .

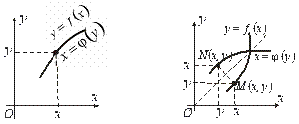
Рис.5.17 Рис.5.18

Функції , різняться лише позначенням змінних. Тому, щоб з графіка функції або, що те саме, функції одержати графік функції , достатньо поміняти ролями всі і , тобто повернути площину рисунка навколо бісектриси першого координатного кута на 1800. Звідси графік відносно бісектриси першого координатного кута (рис.5.18).