Сторінка
5

Поняття множини. Змінні та постійні величини

Якщо точка займе всі можливі положення в області , то пов’язана з нею точка у загальному випадку опише в просторі деяку поверхню . Отже, геометричним зображенням (графіком) функції двох змінних є, в загальному випадку, поверхня в просторі

Геометричне зображення функції трьох і більшого числа змінних не має простого геометричного змісту. В окремих випадках можна отримати наочне геометричне представлення про характер зміни функції, розглядаючи її лінії рівня (або поверхні рівня), тобто лінії (або поверхні), де дана функція зберігає стале значення.

Означення. Лінією рівня функції

називається множина всіх точок площини , для яких дана функція має одне і те саме значення (і зокрема). Отже, рівняння лінії рівня є рівняння , де - довільна стала.

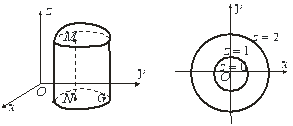
Рис.5.1 Рис.5.2

Приклад. На рис.5.2 зображені лінії рівня функції . Надаючи невід’ємні значення (не може бути від’ємним), одержимо відповідно лінії рівня функції: - точка - коло радіуса з центром

- коло радіуса з центром тощо.

Означення. Поверхнею рівня функції називається множина всіх точок простору для яких ця функція має одне і те саме значення (ізоповерхні).

Лінії і поверхні рівня постійно зустрічаються на практиці. Наприклад, з’єднавши на карті поверхні Землі точки з однаковою середньою температурою або з однаковим середньодобовим тиском, матимемо відповідно ізотерми та ізобари.

5.2.2. Елементарні функції та їх класифікація

Показникова функція (рис.5.3).

Функція означена в інтервалі і неперервна в кожній точці цього інтервалу. При функція зростає; при - спадає. Областю зміни показникової функції є інтервал .

Логарифмічна функція (рис.5.4).

Функція означена в інтервалі і неперервна в кожній точці цього інтервалу. При функція зростає; при - спадає.

Область зміни логарифмічної функції складає множина всіх дійсних чисел.

Степенева функція (рис.5.5, 5.6).

Якщо відносно відомо лише, що це деяке дійсне число, то можна говорити про значення тільки для . Тому в загальному випадку областю означення степеневої функції вважають інтервал . Якщото означена і в точці , де приймає значення . При зростанні степенева функція зростає, якщо і спадає, якщо . Значення у степеневої функції заповнюють інтервал . Якщо число - ціле або дробове з непарним знаменником, то степенева функція при означена для всіх , а при - для всіх , крім .

Тригонометричні функції (рис.5.7, 5.8, 5.9, 5.10).

Функції і мають областю визначення всі

значення змінної . Множиною значень кожної з цих функцій є

відрізок .

Функція означена для всіх значень , крім . Множина значень: .