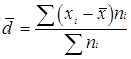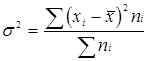Сторінка
8

Статистичне вивчення урожайності зернових

1) Якщо всі частоти ряду розподілу зменшити або збільшити в К‑разів, то середня арифметична при цьому не зміниться.

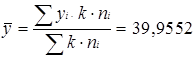
2) Якщо всі значення варіюючої ознаки зменшити або збільшити на одну й ту саму величину, то й середня арифметична зменшиться або збільшиться на ту ж саму величину.

3) Якщо всі значення варіюючої ознаки зменшити або збільшити в одне й те ж число раз, то й середня арифметична зменшиться або збільшиться в таке ж число раз.

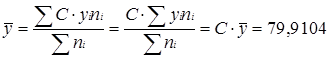
4) Сума відхилень окремих значень варіюючої ознаки від середньої арифметичної дорівнює нулю.

До характеристик центру розподілу крім середньої арифметичної належить мода і медіана. В інтервальному ряді розподілу легко відшукати модальний інтервал, а сама мода визначається за формулою:

, де

у0 – нижня межа модального інтервалу;

h – крок (ширина) інтервалу;

nm – частота модального інтервалу;

nm-1 – частота інтервалу, який передує модальному;

nm+1 – частота інтервалу який слідує за модальним.

Медіана в інтервальному ряді розподілу одчислюється за такою формулою:

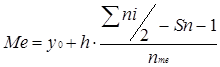, де

у0 – нижня межа медіального інтервалу;

– половина об’єму сукупності;

Sn-1 – сума всіх частот, що передують медіальному інтервалу;

nme – частота медіанного інтервалу.

Таблиця 9. Обчислені показники моди і медіани для згрупованих даних за урожайністю

Статистичні характеристики центру розподілу (середня, мода, медіана) відіграють важливу роль у вивченні статистичних сукупностей. Інколи індивідуальні значення ознаки значно відхиляються від центру розподілу, інколи – тісно групуються навколо нього, а відтак виникає потреба оцінити міру і ступінь варіації.

Таблиця 10. Обчислення показників варіації

Тепер згрупуємо господарства по внесенню органічних добрив. Знайдемо для цієї сукупності середні величини, перевіримо властивості середньої арифметичної, знайдемо моду і медіану для згрупованого ряду розподілу і обчислимо показники варіації.

Таблиця 11. Групування господарств за внесенням органічних добрив