Сторінка
12

Статистичне вивчення урожайності зернових

Знайдемо вибіркову середню:

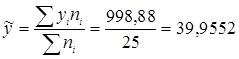
Вибіркова дисперсія буде дорівнювати:

Отже середня помилка вибірки для середньої арифметичної буде дорівнювати:

, t = 2

Підставивши ці дані у формулу граничної помилки вибірки при безповторній вибірці матимемо:

Можливі границі середньої в генеральній сукупності:

Отже з ймовірністю 0,95 можна стверджувати, що різниця між вибірковою і генеральною середніми не перевищує 5,78 ц/га, а середня врожайність знаходиться в межах від 34,14 до 45,74 ц/га.

Таблиця 22. Дані вибіркового обстеження господарств за внесенням органічних добрив

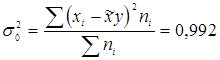
m = 0,19, t = 2

Гранична помилка буде дорівнювати:

Можливі границі середньої в генеральній сукупності:

Отже з ймовірністю 0,95 можна стверджувати, що різниця між вибірковою і генеральною середніми не перевищує 0,39 т/га, а середня величина по внесенню добрив знаходиться в межах від 6,49 до 7,27 т/га.

Таблиця 23. Дані вибіркового обстеження господарств за якістю грунтів

Знайдемо вибіркову середню:

,

Вибіркова дисперсія:

.

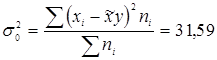Середня помилка для середньої арифметичної:

m = 1,09, t = 2

Гранична помилка:

Можливі границі середньої в генеральній сукупності:

З ймовірністю 0,95 можна стверджувати, що різниця між вибірковою і генеральною середніми не перевищує 2,19 бала, а середня якість грунту знаходиться в межах від 77,45 до 81,83 бала.

3. Статистична оцінка показників генеральної сукупності

Перевіримо відповідність ряду розподілу (У) нормальному закону, використавши критерій c2. Цей показник був введений у статистику К. Пірсоном. За допомогою критерію c2 оцінюють відповідність між фактичним і теоретичним розподілом частот, незалежність розподілу одиницьсукупності за градаціями досліджувальної ознаки, однорідність розподілу.