Сторінка
2

Розклад функцій в степеневий ряд. Достатні умовирозкладу в ряд Тейлора. Застосування степеневих рядів до наближеного обчислення

Формула Маклорена для функції має такий вигляд:

Оскільки то величина при фіксованому обмежена ( при і при ), а, значить

при довільному

Отже, ряд Маклорена для функції має такий вигляд:

(13.56)

який для всіх значень збігається і представляє функцію

Замінивши в розкладі (13.565) на , одержимо ряд

(13.57)

Цими рядами користуються для наближених обчислень значень функцій.

Приклад. Обчислити з точністю

Р о з в ‘ я з о к. Підставляючи в ряд (13.57) замість одержимо

Це знакочергуючий ряд. Оскільки , то з точністю до маємо

13.13. Біноміальний ряд

1. Розклад в ряд функції Розкладемо в ряд функцію де довільне ціле число.

Замітимо, що функція задовольняє диференціальному рівнянню

з початковою умовою

Знайдемо такий степеневий ряд, сума якого задовольняє даному рівнянню з початковою умовою :

.

Підставляючи його в диференціальне рівняння, одержимо

.

Прирівнюючи коефіцієнти при однакових степенях знаходимо:

.

Звідси одержимо коефіцієнти ряду

………………………………………

………………………………………… .

Ці коефіцієнти називаються біноміальними.

Підставляючи їх в ряд, одержимо

.

Якщо ціле додатне число, то, починаючи з члена, що містить всі коефіцієнти дорівнюють нулю і ряд перетворюється в многочлен (біном Ньютона). При дробовому або цілому від’ємному одержимо безмежний ряд. Визначимо його радіус збіжності:

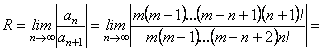
Таким чином, ряд збігається при

В інтервалі даний ряд представляє функцію , що задовольняє даному диференціальному рівнянню з початковою умовою Оскільки дане диференціальне рівняння з початковою умовою має єдиний розв’язок, то сума ряду тотожньо дорівнює функції , і ми маємо розклад функції в ряд:

(13.58)

Ряд (13.58) називається біноміальним рядом.

Зокрема, при одержимо:

(13.59)

При будемо мати:

(13.60)

Біноміальний ряд (13.60) можна використовувати для наближених обчислень значень функцій із заданою точністю.

Приклад. Обчислити з точністю

Р о з в ‘ я з о к. Представимо підкореневе число так і тоді

Підставивши в ряд (13.60) замість а одержимо:

.

Оскільки це знакозмінний ряд , можна оцінити за теоремою Лейбніца залишок ряду

а тому з точністю до маємо:

2. Розклад в степеневий ряд деяких функцій. Застосуємо біноміальний ряд до розкладу інших функцій. Підставивши в ряд (13.59) замість вираз одержимо: