Сторінка
3

Мінімізація затрат ресурсів у проектному менеджменті за допомогою циклічних мережевих моделей

Таким чином, математична модель задачі мінімізації потреби в ресурсах при визначеному часі виконання проекту визначає такі терміни початку і закінчення робіт (m,n) і , що

, для всіх дуг (m,n); (13)

, для всіх t і c; (14)

. (15)

Для обробки сформульованої моделі пропонується алгоритм, в якому замість детермінованих часових параметрів, якими є ранні та пізні терміни здійснення подій, тривалості робіт і довжини дуг, використовуються їх р-квантильні аналоги , , .

Для перерахунку плану ранніх чи пізніх термінів застосовується алгоритм описаний в математичній моделі скорочення часу виконання проекту при ресурсних обмеженнях.

За бажанням користувача вибирається один з варіантів цільової функції , m = 1, 2, …, 6 . Оптимальні плани, отримані за різними критеріями, служать підставою для ухвалення ефективного рішення менеджером проекту.

Роботи, що потрапили в моменти часу, де функціонал приймає максимальне значення, сортуються за спаданням р-квантильних коефіцієнтів напруги .

Роботи вибираються з черги в межах р-квантильних оцінок їхніх резервів, обчислених за відповідними формулами з [3].

Для набору дуг, що виходять з альтернативних вершин, обчислюється – середня інтенсивність споживання c-го ненакопичуваного ресурсу на наборі дуг . Також для набору дуг обчислюється середній коефіцієнт напруги. Далі для включення в план розглядається робота, яка виходить з альтернативної вершини m з обчисленими середніми характеристиками. Якщо ця робота ставиться на обслуговування, то .

У результаті роботи алгоритму ми одержуємо план із заданим рівнем ймовірності р. Збільшуючи кількість ітерацій N, підвищуємо надійність усіх р-квантильних оцінок і, отже, надійність одержаних варіантів плану.

Задачі розподілу обмежених ресурсів на ЦММ розглядалися для випадку постійної інтенсивності виконання робіт. У цьому випадку кількість ресурсів, що використовувалась на кожній роботі ЦММ, була заданою наперед і постійною. У даному пункті припустимо змінну інтенсивність виконання роботи або її частини, а, отже, можливість зміни кількості призначених на неї ресурсів.

Оскільки при описі проекту за допомогою ЦММ ми використовуємо узагальнені зв’язки, що дають змогу виділяти не тільки початки і закінчення робіт як події, але й проміжні стани робіт, то наведена нижче постановка дає змогу реалізувати дві додаткові можливості: вибір інтенсивності виконання всієї роботи ЦММ у заданих межах; зміну інтенсивності виконання окремих частин роботи.

Математична модель задачі розподілу обмежених ресурсів на ЦММ зі змінною інтенсивністю робіт визначає такі терміни початку і закінчення робіт (m,n) 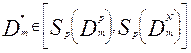і , що

, для всіх дуг (m,n); (16)

, для всіх робіт чи частин робіт (m,n); (17)

, для всіх t і c; (18)

, для всіх і ; (19)

. (20)

Співвідношення (16) задають взаємозв’язки між усіма подіями мережі, включаючи дуги-зв’язки, дуги-роботи і абсолютні часові обмеження.

Співвідношення (17) забезпечують відповідні межі змінної тривалості роботи або її частин, обумовлених формулами: та , де і – відповідно мінімальна та максимальна інтенсивності споживання с-го ненакопичуваного головного ресурсу на роботі (m,n), – трудомісткість виконання роботи (m,n) по головному ресурсу c. Головним ресурсом виступають тільки нескладовані ресурси кількість яких визначає тривалість роботи.