Сторінка
5

Фінансовий ризик

Випадкова величина, яка набуває певних окремих значень, називається дискретною.

Таблиця є прикладом закону розподілу дискретної випадкової величини.

Закон розподілу характеризується кількома показниками, зокрема математичним очікуванням, дисперсією, середньоквадратичним відхиленням, коефіцієнтом варіації.

Математичним очікуванням, або середнім очікуваним значенням випадкової величини Х, називається число, яке дорівнює сумі добутків значень величини (х) на відповідні ймовірності (Рі):

Невизначеність характеризується розсіянням можливих значень випадкової величини довкола її очікуваного значення.

Для характеристик ризику як міри невизначеності використовуються такі показники:

1) дисперсія

D(x) = M[x –M(x)];

2) середньоквадратичне відхилення

1)

коефіцієнт варіації

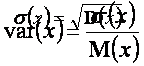Наприклад, для інвестиційного проекту, закон розподілу якого подано в таблиці, ці характеристики становлять:

1) середнє очікуване значення доходу

М(х) = 200 · 0,2 + 800 · 0,5 + 1000 · 0,3 = 740

2) дисперсія

D(x) = (200-740)2 · 0,2 + (800-740)2 ·0,5 + (1000-740)2 · 0,3 = 80400

3) середньоквадратичне відхилення

4) коефіцієнт варіації

Найчастіше як міру ризику використовують середньоквадратичне відхилення. Чим більше його значення, тим більший ризик. Розглянемо інвестиційні проекти А і В, закони розподілу NPV яких задано в таблиці:

Розрахунок середнього очікуваного значення NPV для двох проектів

Проект А		Проект В
Можливі значення NPV (ХА)	Відповідні ймовірності (РА)	Можливі значення NPV (ХВ)	Відповідні ймовірності (РВ)
100 500 700 1500	0.2 0.4 0.3 0.1 760	-7200 1000 3000 5000	0.2 0.3 0.3 0.2 760

М (ХА) = 100 · 0,2 + 500 · 0,4 + 700 · 0,3 + 1500 · 0,1 = 760

М (ХВ) = -7200 · 0,2 + 1000 · 0,3 + 300 · 0,3 + 5000 · 0,2 = 760

Тобто, очікуване значення NPV для обох проектів однакове. Втім, величини їх середньоквадратичного відхилення істотно різняться:

D (ХА) = (100-760)2 · 0,2 + (500-760)2 · 0,4 + (700-760)2 · 0,3 + (1500- 760)2 · ·0,1 = 170000

D (ХB) =(-7200 – 760)2 · 0,2 + (1000 –760)2 · 0,3 + (3000 – 760)2 · 0,3 + (5000 – 760)2 ·0,2 = 17790400

σ(хВ) значно більше σ(хВ), а отже, ризик проекту В вищий від ризику проекту А.

Якщо порівнюються два проекти з різними очікуваними значеннями NPV, то використовується коефіцієнт варіації, який показує частку ризику на одиницю очікуваного значення NPV.

Основною ідеєю аналізу рівня власного ризику проекту є оцінка невизначеності очікуваних грошових потоків від даного проекту. Цей аналіз може бути проведений різними методами – від неформальної інтуїтивної оцінки проекту до складних розрахункових методів та використання статистичного аналізу й математичних моделей.

Практично всі розрахункові значення грошових потоків, на яких заснований проектний аналіз, є очікуваними значеннями випадкових величин з певними законами розподілу. Ці розподіли можуть мати більшу чи меншу варіацію, що є відображенням більшої чи меншої невизначеності, тобто ступеня власного ризику проекту. Характер розподілу ймовірностей грошових потоків та їх кореляції одного з одним зумовлює характер розподілу ймовірностей NPV проекту і, таким чином, рівень власного ризику даного проекту.

У випадках, коли ризик розрахувати неможливо, прийняття ризикових рішень відбувається за допомогою евристики, що являє собою сукупність логічних прийомів і методичних правил теоретичного дослідження і відшукання істини. Іншими словами, це способи рішення особливо складних задач. Ризик-менеджмент має свою систему евристичних правил і прийомів для ухвалення рішення в умовах ризику: - Не можна ризикувати більше, ніж це може дозволити власний капітал. - Завжди треба думати про наслідки ризику. - Позитивне рішення приймається лише при відсутності сумніву. - Не можна ризикувати великою кількістю заради малого. - При наявності сумніву приймаються негативні рішення. - Не можна думати, що завжди існує тільки одне рішення, можливо, що є й інші варіанти.

Перш ніж прийняти рішення про ризикове вкладення капіталу, фінансовий менеджер повинен визначити максимальний обсяг збитку по даному ризику; зіставити його з обсягом вкладеного капіталу; порівняти його з усіма власними фінансовими ресурсами і визначити, чи не приведе втрата цього капіталу до банкрутства інвестора. Обсяг збитку від вкладення капіталу може бути дорівнює обсягу даного капіталу, бути менше його чи більше.

Невід'ємним елементом ризику-менеджменту є організація заходів щодо виконання наміченої програми, тобто визначення окремих видів заходів, обсягів і джерел фінансування цих робіт, конкретних виконавців, термінів виконання і т.д. Важливим етапом організації ризику-менеджменту є контроль за виконанням наміченої програми, аналіз і оцінка результатів обраного варіанта ризикового рішення. У стратегії ризику-менеджменту застосовуються наступні правила: