Сторінка
4

Розвиток креативних здібностей через систему креативних вправ

Впевнившись у правильності розв'язування і, якщо потрібно, виконавши дослідження задачі, необхідно чітко сформулювати відповідь - це буде сьомий етап процесу розв'язування.

Нарешті, в навчальних і пізнавальних цілях корисно також провести аналіз виконаного розв'язування, тобто встановити, чи нема іншого, більш раціонального способу розв'язування, чи не можна задачу узагальнити, які висновки можна зробити із цього розв'язування. Все це складає останній - восьмий етап розв'язування.

Математичні задачі, для розв'язування яких в шкільному курсі математики існують готові правила, або ці правила безпосередньо випливають з означень чи теорем, що визначають програму розв'язування цих задач у вигляді послідовності кроків, називають стандартними. При цьому передбачається, що для виконання окремих кроків розв'язування стандартних задач в курсі математики існують конкретні правила.

Процес розв'язування стандартних задач має деякі особливості.

1. Аналіз задач зводиться до встановлення (розпізнавання) виду задач, до якого належить дана задача.

2. Пошук розв'язування полягає у складанні на підставі загального правила (формули, тотожності) або загального положення (означення, теореми) програми – послідовності кроків розв'язування задач даного виду. Звичайно, немає необхідності цю програму формулювати в письмовій формі, достатньо її для себе намітити усно.

3. Саме розв'язання стандартної задачі полягає у застосуванні цієї загальної програми до умови даної задачі. Якщо деякі кроки програми розв'язування вимагають для свого виконання використання також інших програм, то стосовно них проводяться ті самі операції (розпізнавання виду задачі, складання програми розв'язування і виконання розв'язування на основі цієї програми). Звідси походить, що для того щоб легко розв'язувати стандартні задачі (а вони є основними математичними задачами, оскільки всі інші зрештою зводяться до них), треба:

1) пам'ятати всі вивчені в курсі математики загальні правила (формули, тотожності) і загальні положення (означення, теореми);

2) вміти розгортати згорнуті загальні правила, формули, тотожності, а також означення і теореми у програмі - послідовності кроків розв'язування задач відповідних видів.

У визначенні стандартних задач як основну ознаку цих задач вважають наявність в курсі математики таких загальних правил чи положень, які однозначно визначають програму розв’язання цих задач і виконання кожного кроку цієї програми.

Звідси зрозуміло, що нестандартні задачі - це такі задачі, для яких в курсі математики немає загальних правил і положень, що визначають точну програму їх розв’язування.

Процес розв’язування будь-якої нестандартної задача складається у послідовному застосуванні двох основних операцій:

1. Зведення (шляхом перетворення або переформулювання) нестандартної задачі до іншої, їй еквівалентної, але уже стандартної задачі;

2. Розбиття нестандартної задачі на декілька стандартних підзадач.

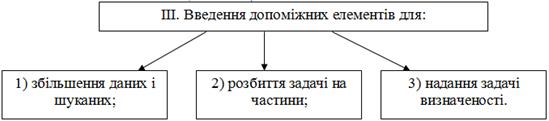
В залежності від характеру нестандартної задачами використовуємо одну із цих операцій або обидві. При розв'язуванні більш складних задач ці операції доводиться застосовувати багаторазово. Розглянемо методи розв’язання нестандартних задач і покажемо це у вигляді наступної схеми.

Відомо, що будь-який урок — це складне педагогічне явище, витвір вчителя, на якому учні демонструють свої знання, уміння та навички.

Чи цікаво дітям на уроці? Чи люблять вони вчитися?

На ці питання не можна відповісти напевне. Іноді діти ідуть на урок із задоволенням, іноді без нього. Як зацікавити дітей? Як привернути їх увагу до свого предмету? Звичайно, за допомогою того, що їм буде слухати найцікавіше, того, що вони будуть робити із задоволенням.

Як донести матеріал до їх свідомості яскраво і красиво, щоб запам'яталось надовго і назавжди?

Іноді можна почути, що математика складна, суха і нецікава наука. Людей, які люблять математику, це вражає й ображає. Математика сувора, але красива й глибока, як чиста криниця. А завдання — вчителя і полягає в тому, щоб розкривати перед учнями її емоційний бік, чуйну і вродливу стать. Як краще цього домогтися?

Красивими, цікавими уроками. Уроками, які пробуджують цікавість і працьовитість, фокусують увагу і зосередженість. Отже, нестандартний урок. Він не вкладається в рамки виробленого і сформульованого дидактикою. На цьому уроці можна не дотримуватись чітких етапів навчального процесу, методів, традиційних видів роботи. Для такого уроку характерною є інформаційно-пізнавальна система навчання — оволодіння готовими знаннями, пошук нових форм викладу, розкриття внутрішньої сутності явищ через гру, змагання або нетрадиційні форми роботи з дітьми, використовувати власні дидактичні матеріали, часто саморобні і тим більше корисні для учнів.

Позакласна робота з математики дуже важлива для пробудження в учнів інтересу до математики. Тому математичні вікторини, змагання, ігри, прес-конференції, вечори сприяють підвищенню математичної культури, розширюють і поглиблюють здобуті на уроках знання, показують застосування їх на практиці, розвивають мислення, креативні математичні здібності, допомагають ввійти у світ наукових і технічних ідей. Щоб розвинути креативні здібності учнів, поступово та систематично залучати до самостійної пізнавальної діяльності, щоб забезпечити співпрацю між учнями та учителем, традиційного уроку недостатньо. Тому для розвитку креативних здібностей особливу увагу в даній курсовій роботі приділяється не позакласній роботі і урокам, а креативним вправам.

Розробка методики розвитку креативних здібностей через систему креативних вправ

Школа має своїм завданням не лише озброїти учнів міцними знаннями, а й формувати в них досвід творчої діяльності.

Розвиток креативного мислення через систему креативних вправ передбачає:

Ø творчий підхід до розв’язання стандартних вправ;

Ø розв’язання нестандартних вправ;

Ø варіативність під час розв’язування задач і вправ;

Ø виховання навичок дослідницької діяльності через систему креативних завдань;

Ø розв’язання творчих вправ під час повторення вивченого матеріалу.

Розвитку креативних здібностей учнів сприяє цілеспрямоване і систематичне включення творчих вправ і завдань у навчальний процес. Це дає змогу наблизити навчальну діяльність до наукової, підвищити ефективність навчання математики в загальноосвітній школі. Перш за все вчитель повинен навчати творчого підходу до розв’язання стандартних вправ.

Приклад 1. Розв’яжіть рівняння

Його, звичайно, можна розв’язати так: знайти нулі підмодульних виразів, розбити числову пряму на проміжки і розкривати модулі на кожному з проміжків. За допомогою міркувань підводимо учнів до другого способу: врахуємо, що отже, (оскільки за іншої умови рівняння не буде мати коренів). При такому значенні х: і Дістанемо систему: