Сторінка
3

озробка учбового матеріалу для викладання вищої математики на тему "Наближені методи обчислення визначених інтегралів"

2) Коли , то застосовуєма форма квадратурних рівнянь називається - „квадратурна формула Симпсона”;

3) Коли , формула (1.19) не застосовується, оскільки значення не визначені, тому застосовується особливий випадок „квадратурної формули прямокутників (ліві, праві, центральні) ".

Чисельні методи інтегрування

Метод прямокутників

Нехай є відрізок і нам треба обчислити визначений інтеграл

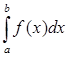(2.1 1)

за попередньо представленою загальною квадратурною формулою Н’ютона - Котеса (1.4)

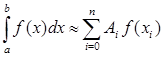(2.1 2)

де - деякі фіксовані вузли

Найпростіший варіант інтерполяційної квадратурної формули (2.1 2) виникає, коли . У цьому випадку не можна скористатися формулою (1.20), бо коефіцієнт (1.19) при невизначений. Тому, як і при побудові загальної інтерполяційної формули, замінимо підінтегральну функцію інтерполяційним багаточленом нульового степеня, що побудований за єдиним вузлом .

(2.1 3)

при заміні підінтегральної функції (2.1 2) інтерполяційним поліномом нульового степеня, що побудований по єдиному вузлу

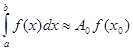(2.1 3)

Знайдемо коефіціент

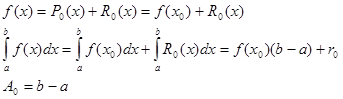(2.1 4)

Після інтегрування маємо квадратурну „формулу прямокутника”:

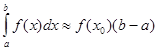,(2.1 5)

Приїї називають формулою лівих прямокутників,

Приїї називають формулою правих прямокутників,

При- центральних (або середніх) прямокутників.

Геометричне тлумачення цієї формули показано на рис 2.1

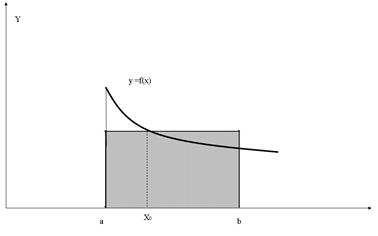
Рис.2.1 Геометричне зображення „формули прямокутників"

Оцінимо похибку квадратурної формули (2.1 5) за умови, що . За означенням похибки квадратурної формули (2.1 5) маємо

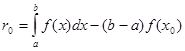(2.1 6)

Функцію запишемо у вигляді розвинення в ряд Тейлора в околі точки [7]:

(2.1 7)

Проінтегруємо обидві частини рівності (2.1 7) по відрізку

(2.1 8)

Тепер підставимо інтеграл (2.1 8) в (2.1 6)

(2.1 9)

Тепер розглянемо конкретні варіанти вибору точки

При (праві прямокутники): (2.1 10)

При (ліві прямокутники): (2.1 11)

При- (центральні прямокутники): (2.1 12)

З формул (2.1 10), (2.1 11), (2.1 12) видно, що алгебраїчний степінь точності формули центральних прямокутників на 1 вище ніж лівих або правих.

Якщо довжина відрізку велика, то формули прямокутників мають невисоку точність. У цих випадках краще користуватися сумарними формулами прямокутників. Для цього розіб‘ємо відрізок на рівних частин з кроком . Інтеграл шукаємо як суму інтегралів по всіх цих відрізках, тобто

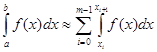(2.1 13)

На кожному відрізку інтеграл обчислюємо, користуючись однією з квадратурних формул прямокутників. Розглянемо окремі випадки.

1. „Ліві прямокутники"

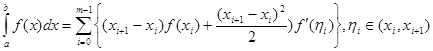. (2.1 14)

В останній формулі (2.1 14) враховано не тільки наближені значення інтегралів за формулою (2.1 5), але й залишки за формулою (2.1 9). Тепер в правій частині цієї рівності запишемо окремо суму наближених значень інтегралів та суму залишків

(2.1 15)

Приймемо до уваги неперервності функції на . Нехай

тоді існує така точка , що буде вірною рівність

Тепер з формули (2.1 15) маємо остаточно узагальнену формулу „лівих прямокутників”:

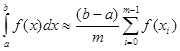(2.1 16)

та похибку цієї формули

(2.1 17)

Геометричне зображення „формули лівих прямокутників" наведене на рисунку (2.2)

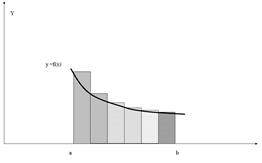
Рис.2.2 Геометричне зображення „формули лівих прямокутників"

2. Аналогічно для квадратурної формули „правих прямокутників" отримуємо узагальнену формулу

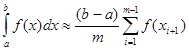(2.1 18)

та похибку

(2.1 19)

Геометричне зображення „формули правих прямокутників" наведене на рисунку (2.3).