Сторінка
4

озробка учбового матеріалу для викладання вищої математики на тему "Наближені методи обчислення визначених інтегралів"

Рис.2.3 Геометричне зображення „формули правих прямокутників”

3. Узагальнена квадратурна формула „центральних прямокутників" запишеться у вигляді:

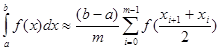(2.1 20)

її залишок має вигляд

(2.1 21)

Геометричне зображення „формули центральних прямокутників" наведене на рисунку (2.4).

Рис.2.4 Геометричне зображення „формули центральних прямокутників"

2.2 Метод трапецій

Квадратурна „формула трапеції” - це виключний випадок формули Н’ютона - Котеса (1.20), коли . Квадратурна формула трапеції має вигляд:

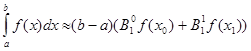(2.2.1)

Два коефіцієнти Котеса знаходимо, враховуючи їхні властивості

Тоді формула трапеції має вигляд

(2.2.2)

Геометричне тлумачення наведене на рис.2.5 Геометрично цю формулу отримаємо, якщо криву замінити хордою, яка проходить через точки та , тоді інтеграл знаходиться як площа трапеції .

Рис.2.5 Геометричне тлумачення „формули трапецій”

Формула (2.2.2) наближена. Визначимо похибку для квадратурної формули трапеції:

Похибка квадратурної формули (2.2.2) випливає з (1.12), якщо взяти та

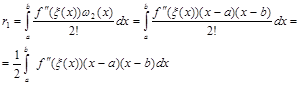
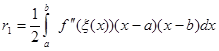(2.2.3)

До обчислення останнього інтеграла застосуємо теорему про середнє.

Теорема. Нехай - інтегровані на проміжку функції, причому , на всьому проміжку не змінює знак. Тоді

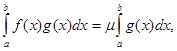де

Якщо неперервна на , то ця формула може бути записана у вигляді

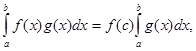де

Застосуємо цю теорему до інтеграла (2.2.3). За припущенням функція є неперервною на , тому знайдеться така точка , що буде виконуватися рівність.

Отже,

(2.2.4)

Якщо відрізок достатньо великий, то похибка (2.2.4) квадратурної формули трапеції, як правило, велика. Для збільшення точності розділимо відрізок інтегрування на частин точками , тоді

Якщо розбиття рівномірне, тобто , то

Запишемо окремо узагальнену формулу трапеції і окремо її похибку:

(2.2.5)

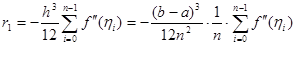(2.2.6)

Величина -середнє арифметичне значень другої похідної в точках відрізку . Очевидно, що , де -найменше значення, а -найбільше значення другої похідної , . Оскільки неперервна на , то в якості своїх значень на вона приймає всі проміжні числа між і . Отже, існує така точка , що , тобто

(2.2.7)

На рис (2.6) показано геометричне зображення узагальненої формули трапеції (2.2.5).

Рис.2.6 Геометричне зображення узагальненої формули трапецій

Точне значення інтеграла, тобто ліва частина наближеної рівності (2.2.5) це площа криволінійної трапеції, що обмежена зверху графіком функції . Наближене значення інтеграла (права частина рівності (2.2.5) - це площа фігури, що зверху обмежена ламаною (рис.2.6).

З формули (2.2.7) видно, що чим більшим є число , тим меншою буде похибка квадратурної формули (2.2.5). Крім того, з (2.2.7) видно, що алгебраїчний степінь точності і квадратурної формули трапеції дорівнює одиниці (так же, як і формули центральних прямокутників).

Метод Симпсона

Якщо в квадратурній формулі Ньютона-Котеса (2.12) взяти то здобудемо таку формулу

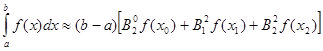(2.3.1)