Сторінка
3

Визначення проектних ризиків

Одноперіодні грошові потоки. Для ілюстрації показників ризику для одноперіодних грошових потоків можна використати інформацію, наведену в табл. 7.2.

Таблиця 7.2

Середнє квадратичне (стандартне) відхилення. Як зазначалося раніше, очікувана вартість не є сама по собі прийнятним критерієм, оскільки вона не враховує таку важливу інформацію, як дисперсія (ризик) стосовно результатів. Можна стверджувати, що різні люди в ризикованих ситуаціях поводяться по-різному. Розглянемо проекти А і Б та їхній розподіл NPV, який наведено на рис. 7.3.

Обидва проекти мають одну й ту саму чисту теперішню вартість, але проект А має більшу дисперсію. Особа, схильна до ризику, намагаючись його мінімізувати, вибере варіант Б. Любитель ризику віддасть перевагу варіанту А, тому що показник NPV за цим проектом має шанс (W) бути вищим ніж Х (чого не може запропонувати проект Б), але також і шанс L бути нижчим ніж Y. Неможливо спрогнозувати вибір особи без знання її ставлення до ризику. На майбутнє можна зробити справедливе припущення, що особа не схильна до ризику. Середнє квадратичне (стандартне) відхилення є мірою дисперсії: чим ширша дисперсія, тим вище середнє квадратичне (стандартне) відхилення. Очікувана вартість грошових потоків розраховується за такою формулою:

,

де — очікуване значення події Х;

N — кількість можливих наслідків;

Хі — можливий наслідок від події Х;

Рі — імовірність наслідку події і.

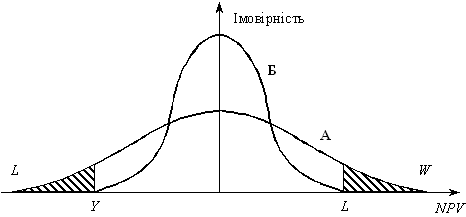
Рис. 7.3. Розподіл NPV для проектів А і Б

Середнє квадратичне (стандартне) відхилення грошових потоків (s) становить:

.

У табл. 7.3 наведено розрахунки для проектів А і Б.

Використовуючи формули, ми отримуємо очікуваний грошовий потік у розмірі 400 грн як для проекту А, так і для проекту В. Якщо особа, що приймає рішення, ставиться до ризику нейтрально, для неї обидва проекти будуть однаково прийнятними. Але якщо схоже, що особа не схильна до ризику, тоді варто розглянути середнє квадратичне (стандартне) відхилення двох розподілів імовірностей. Тут можна побачити, що проект А має середнє квадратичне відхилення, яке вдвічі більше за значення середнього квадратичного відхилення для проекту Б, і, отже, проект А є більш ризиковим, а значить, і менш привабливим. До такого висновку можна прийти, просто аналізуючи розподіл наслідків (результатів) та маючи на увазі, що обидва проекти мають одні й ті самі показники ймовірностей. Проте такий аналіз не дає відповіді, наскільки один проект є більш або менш ризиковим за інший.

Таблиця 7.3