Сторінка
5
І — інвестиційні витрати;
r — безризикова процентна ставка.
Незв’язані грошові потоки. Головною проблемою за розрахунку середньоквадратичного (стандартного) відхилення значення NPV для багатоперіодних проектів є те, що грошові потоки в одному періоді частково залежні від грошових потоків попередніх періодів. Припускаючи, на поточний момент, що грошові потоки нашого двохперіодного проекту є статистично незалежними, загальна варіація NPV дорівнює дисконтованій сумі річних варіацій. Це можна проілюструвати на такому прикладі: припустимо, що проект, тривалість якого становить два роки, має початкові витрати 500 грн, а можливі виплати та ймовірності наведено в табл. 7.4.
Таблиця 7.4
ІМОВІРНІСТЬ РЕАЛІЗАЦІЇ ГРОШОВИХ ПОТОКІВ ПРОЕКТУ
| Імовірність | Рік 1 Грошовий потік | Рік 2 Грошовий потік |
| 0,1 | 100 | 200 |
| 0,2 | 200 | 400 |
| 0,4 | 300 | 600 |
| 0,2 | 400 | 800 |
| 0,1 | 500 | 1000 |
Використовуючи середньоквадратичне відхилення й формулу очікуваної вартості, ми матимемо:
|
Показник |
Рік 1 |
Рік 2 |
|
Очікувана вартість (грн) |
300 |
600 |
|
Стандартне відхилення (грн) |
109 |
219 |
Припускаючи, що безризикова ставка дисконтування 10 %, очікувана NPV становитиме:
 ,
,
![]()
Середньоквадратичне (стандартне) відхилення за цим проектом знаходиться дисконтуванням річних варіацій до їхньої теперішньої вартості з використанням такої формули:
 .
.
У нашому простому випадку:
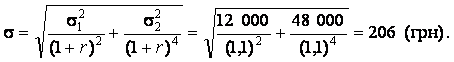
Отже, проект пропонує очікувану NPV 268 грн. та середньоквадратичне відхилення 206 грн.
Прямолінійно корельовані грошові потоки. Іншою крайністю щодо статистичної незалежності між періодами є припущення, що грошові потоки одного періоду є повністю залежними від грошових потоків попередніх періодів. Коли таке трапляється, то кажуть, що вони прямолінійно корельовані. Будь-яке відхилення від прогнозу в одному році безпосередньо впливає на точність наступних прогнозів. Результат того, що грошові потоки корелюються протягом певного часу, полягає в тому, що середньоквадратичне (стандартне) відхилення розподілу ймовірності чистої теперішньої вартості збільшується. Середньоквадратичне (стандартне) відхилення протікання прямолінійно корельованих у часі грошових потоків визначається за такою формулою:
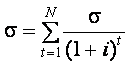 .
.
Повертаючись до прикладу, наведеного в табл. 7.4, але зважаючи на наявність прямолінійної кореляції грошових потоків у часі, середньоквадратичне (стандартне) відхилення проекту становитиме:

Отже, ризик, пов’язаний із цим двохперіодним проектом, за умови прямолінійної кореляції становить 280,6 грн. Попередні розрахунки за умови незалежності грошових потоків дають менше значення середньоквадратичного (стандартного) відхилення в розмірі 206 грн. Очевидно, що ця різниця буде значно більшою для триваліших проектів.
Інтерпретація результатів
Особа, яка приймає рішення, хоча й зацікавлена в тому, щоб отримати значення показника рівня ризику, що пов’язаний із проектом, її основною турботою є відповідь на питання: «Чи буде проект продукувати позитивну теперішню вартість?». Аналіз ризику може певним чином допомогти вирішити це питання. Якщо розподіл імовірності, очікуваної від проекту NPV, є наближеним до нормального, тоді можна оцінити ймовірність невдачі за досягнення нульового значення NPV. У попередньому прикладі очікувана NPV становила 268 грн. Потім її нормують діленням на середньоквадратичне (стандартне) відхилення за такою формулою:
 ,
,
де в даному випадку Х = 0. Отже, за припущення існування незалежних грошових потоків, стандартне відхилення становитиме:
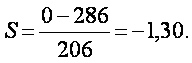
З таблиць нормального розподілу можна визначити, що ймовірність того, що NPV £ 0, становить 0,0968. Згідно з цим, можливість, що проект продукуватиме NPV більшу за нуль, становитиме (1 – 0,0968), або 90,32 %. Особа, яка приймає рішення, може потім експертним шляхом співвіднести цей рівень ризику з власною функцією корисності перед тим, як приймати рішення.
