Сторінка
4

Визначення проектних ризиків

Половинна дисперсія. Деякі фахівці зауважують, що, не зважаючи на те, що відхилення вищі середнього, підприємець може сприймати як позитивні, це тільки нижня межа ризику, що розглядається в процесі прийняття рішень. Найкраще вона може бути визначена за допомогою половинної дисперсії, що розраховується за формулою:

,

де SV — половинна дисперсія;

j — усі значення X, які менші за очікуване;

K — кількість наслідків, значення яких менше за очікуване.

Використавши формулу половинної дисперсії до попереднього прикладу, можна зробити висновок, що ризик нижньої межі стосується лише слабкого стану економіки:

SVА = 0,3(200 – 400)2 = 12 000 (грн),

SVБ = 0,3(300 – 400)2 = 3000 (грн).

Отже, проект Б має значно нижчий рівень ризику. В обох випадках половинна дисперсія становить 40 % дисперсії за проектом (12 000/30 000 та 3000/7500 відповідно).

Коефіцієнт варіації. Не можна вважати повністю задовільним безпосереднє порівняння проектів, що здійснюється на основі визначення абсолютних показників ризику, так як це робилося раніше. Там, де проекти відрізняються за масштабом, можна використати достовірніший відносний показник ризику, такий як коефіцієнт варіації (CV). Він розраховується як співвідношення середнього квадратичного (стандартного) відхилення й очікуваної величини чистого грошового потоку:

.

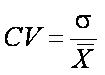У нашому прикладі з табл. 7.3 можна розрахувати такі значення коефіцієнта варіації:

Проект А 173,2/400 = 0,43

Проект Б 86,6/400 = 0,22

Оскільки в цьому випадку обидва проекти мають однакові значення очікуваних грошових потоків, то й результати не відріз­нятимуться від отриманих за двома попередніми методиками аналізу: у всіх трьох випадках проект Б має значно нижчий рівень ризику, але одну й ту саму очікувану вартість. Проте в наступному прикладі два проекти, що розглядаються, відрізняються один від одного за масштабом.

Хоча абсолютна величина дисперсії (стандартного відхилення) за проектом Г є більшою, підприємець може розцінити його як більш ризиковий, ніж проект В, з огляду на значну різницю в очікуваних вартостях цих двох інвестиційних проектів. Коефіцієнт варіації показує, що проект Г насправді пропонує нижчий показник ризику на 1 гривню очікуваної вартості.

Правило середньої варіації. Знаючи очікуваний дохід, а також величину дисперсії (варіації або стандартного відхилення), можна сформулювати прикладне правило середньої варіації, за яким проекту Х віддається перевага перед проектом Y, якщо є правдивим хоча б одне з таких тверджень:

1) очікуваний дохід від проекту Х перевищує дохід від проекту Y, а значення варіації є однаковим, або ж для проекту Х воно менше, ніж для проекту Y;

2) очікуваний дохід від проекту Х перевищує або має ту саму величину, що й від проекту Y, а варіація за проектом Х є менша, ніж за проектом Y.

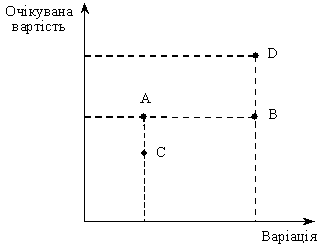
Рис. 7.4. Вибір проектів за правилом середньої варіації

Це проілюстровано на рис. 7.4. Проектам А і D завжди буде надано перевагу перед проектами С і В, беручи до уваги, що вони пропонують вищий дохід за одного й того самого рівня ризику. Крім того, проект А є більш привабливим, ніж проект В, оскільки за одного й того самого значення очікуваного доходу проект А має нижчий рівень ризику. Важливість правила середньої варіації полягає в тому, що воно прийнятне для використання всіма особами, не схильними до ризику, без урахування їхніх індивідуальних функцій корисності. Але це правило не спрацьовує, якщо проекти різняться між собою за показниками очікуваного доходу й ризику (проекти А і D на рис. 7.4).

Багатоперіодні грошові потоки. В усіх попередніх випадках розглядалися одноперіодні інвестиції. Для спрощення ігнорувався факт, що типова інвестиція є багатоперіодною. Тому наш аналіз має базуватися на показнику чистої теперішньої вартості. З огляду на те, що ризик оцінюється окремо, грошові потоки повинні бути оцінені за безризиковою процентною ставкою, що відображає лише вартість грошей у часі. Включення премії за ризик у ставку дисконтування, коли показник ризику розраховано окремо, призводить до подвійного його врахування й, отже, штуч­но зменшує чисту теперішню вартість. Очікувана чиста теперішня вартість інвестиційного проекту знаходиться додаванням вартостей очікуваних грошових потоків та відніманням початкових інвестиційних витрат. Отже, для інвестиційної пропозиції тривалістю два роки

,

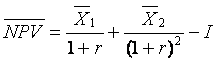де — очікувана NPV;

— очікувана величина чистого грошового потоку року 1;

— очікувана величина чистого грошового потоку року 2;