Сторінка
3
![]() ,
,
або
![]() ,
,
де ![]() - середній радіус між
- середній радіус між ![]() і
і ![]() .
.
Припускаючи, що функція ![]() неперервна в області
неперервна в області ![]() , складемо для неї інтегральну суму , вибираючи точки
, складемо для неї інтегральну суму , вибираючи точки ![]() в областях
в областях ![]() так, щоб вони лежали на середніх колах радіуса
так, щоб вони лежали на середніх колах радіуса ![]() , тобто покладемо
, тобто покладемо![]() . Тоді інтегральна сума запишеться так :
. Тоді інтегральна сума запишеться так :
![]() .
.
У правій частині стоїть інтегральна сума для функції
|
|
Рис.11.8 Рис.11.9
![]() за змінними
за змінними ![]() і
і ![]() , а тому, переходячи до границі, дістанемо
, а тому, переходячи до границі, дістанемо
![]() . (11.20)
. (11.20)
Це і є формула перетворення подвійного інтеграла від декартових координат ![]() до полярних
до полярних ![]() . Вираз
. Вираз ![]() називається елементом площі.
називається елементом площі.
Обчислення подвійного інтеграла в полярній системі координат, як і в декартовій, зводиться до послідовного інтегрування за змінними ![]() і
і ![]() .
.
Вкажемо правила розстановки меж інтегрування.
1. Нехай полюс лежить за областю інтегрування ![]() , а сама область поміщена між променями
, а сама область поміщена між променями ![]() та
та ![]() і координатні лінії
і координатні лінії ![]() зустрічають її межу не більше як у двох точках (рис.11.9). Припустимо, що полярні рівняння кривих
зустрічають її межу не більше як у двох точках (рис.11.9). Припустимо, що полярні рівняння кривих ![]() і
і ![]() .
.
Інтегруючи спочатку за ![]() у межах його зміни за сталою
у межах його зміни за сталою ![]() , тобто від
, тобто від ![]() до
до ![]() , а потім за
, а потім за ![]() від
від ![]() до
до ![]() , дістанемо
, дістанемо
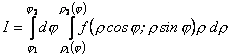 . (11.21)
. (11.21)
У частинному випадку , якщо область інтегрування є частина кругового кільця ![]() , то межі інтегрування сталі за двома змінними
, то межі інтегрування сталі за двома змінними
 . (11.22)
. (11.22)
2. Нехай полюс лежить в області інтегрування ![]() і будь-який полярний радіус перетинає її межу в одній точці. Інтегруючи спочатку за
і будь-який полярний радіус перетинає її межу в одній точці. Інтегруючи спочатку за ![]() , а потім за
, а потім за ![]() , дістаємо
, дістаємо
|
|
 , (11.23)
, (11.23)
де ![]() - полярне рівняння межі області
- полярне рівняння межі області ![]() .
.
Частково, при ![]() , тобто , якщо область інтегрування є круг з центром в полюсі, то
, тобто , якщо область інтегрування є круг з центром в полюсі, то
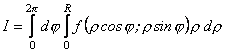 . (11.24)
. (11.24)
Отже, щоб перейти в подвійному інтегралі від декартової системи координат до полярної і обчислити його, необхідно:
1) записати межу області ![]() у полярних координатах;
у полярних координатах;
2) замінити аргументи ![]() та
та ![]() підінтегральної функції відповідно на
підінтегральної функції відповідно на ![]() і
і ![]() ;
;
3) замінити елемент площі ![]() на
на ![]() ;
;
4) розставити межі інтегрування по області ![]() ;
;
5) обчислити повторний інтеграл.
Приклад. За допомогою переходу до полярних координат обчислити подвійний інтеграл ![]() де область
де область ![]() частина кільця (рис. 11.10).
частина кільця (рис. 11.10).
Р о з в ‘ я з о к.
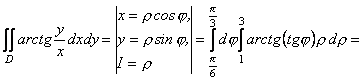
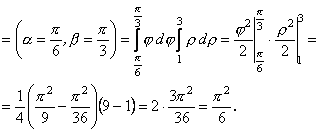
Інші реферати на тему «Математика»:
Векторна функція скалярного аргументу. Похідна, її геометричний і механічний зміст. Кривизна кривої
Інтерполяція
Визначення та обчислення довжини дуги плоскої кривої в декартових та полярних координатах. Площа поверхні
Джерела статистики, види середніх та способи їх обчислення
Поняття множини. Змінні та постійні величини


