Сторінка
2

Інтегрування раціональних функцій

Згідно з теоремою Вієта поліном розкладається на множники вигляду , де - корені полінома, тобто

Нехай і - комплексно спряжені корені. Тоді їм відповідатиме в розкладі два множники і . Їх добуток

Отже, кожній спряженій парі комплексних коренів відповідає множник вигляду . Серед коренів полінома можуть виявитися кратні. Якщо врахувати це, то розклад полінома на множники запишеться так:

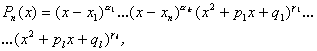(8.21)

де - кратності дійсних коренів, - кратності пар комплексно спряжених коренів.

Нехай правильний дріб має вигляд , де і – степені поліномів і і розкладається на множники так, як це показано в (8.21). У курсі алгебри доводиться, що кожному простому дійсному кореню відповідає простий дріб , а - кратному відповідає сума простих дробів:

Кожній парі комплексно спряжених коренів відповідає простий дріб вигляду , де кожній - кратній парі комплексно спряжених коренів відповідає сума простих дробів:

Розглянемо конкретний приклад розкладу на прості дроби правильного раціонального дробу

в якому знаменник уже розкладений на множники. Коренями знаменника є однократний корінь 1, двократний корінь 2, двократна пара комплексно спряжених коренів (корені рівняння ), однократна пара комплексно спряжених коренів (корені рівняння ).

Отже , заданий дріб може бути поданий як

де - невідомі коефіцієнти , які треба обчислити, виходячи з того, що написана рівність є тотожністю. Її можна записати , звільнившись від знаменників:

Якщо прирівняємо коефіцієнти за однакових степенів у правій і лівій частинах одержаної тотожності після того, як у правій частині будуть виконані дії і згруповані члени з однаковими степенями , то одержимо систему дев’яти лінійних рівнянь із дев’ятьма невідомими відносно невідомих коефіцієнтів, які й знайдемо із вказаної системи рівнянь. У курсі алгебри доведено, що необхідна система рівнянь для визначення невідомих коефіцієнтів завжди має єдиний розв’язок .

Але можна зробити інакше : в написану тотожність замість по черзі підставити корені знаменника дробу ( хоч можна замість підставляти довільні числа.). В результаті одержимо шість невідомих коефіцієнтів. Отже, залишиться знайти ще три коефіцієнти .

При , а при , при матимемо , Звідси дістаємо систему рівнянь з якої знаходимо . При аналогічно знайдемо . Отже, залишилися невідомими . Їх можна знайти, підставляючи в тотожність замість , наприклад, . Із врахуванням значень з системи трьох лінійних рівнянь з трьома невідомими можна визначити .