Сторінка
2

Деякі аспекти використання теорії ігор в адмініструванні податків

Умови гри зазвичай записуються у формі платіжної матриці Q(qij) (рис.1), рядки якої відповідають стратегіям одного гравця (наприклад, органи державної податкової служби в особі податкового інспектора), а стовпчики – іншого (наприклад, платник податків).

Рис. 1. Вигляд платіжної матриці гри

Елементи матриці qijвизначають виграш одного гравця (і відповідно програш іншого), якщо він обере стратегію і (i = 1, ., m ), а інший – стратегію j (j = 1, ., n).

Функція виграшу Q(qij) при можливих комбінаціях стратегій гравців повинна бути визначена на основі детального аналізу інформації про роботу суб’єкта підприємницької діяльності (обсяги реалізації, хронічна неприбутковість тощо) за попередні періоди, накопиченої у базах даних автоматизованої інформаційної системи АІС “Податки”.

Кожна гра має нижню та верхню ціну гри, що відображає мінімальний виграш та максимальний програш при визначеній оптимальній стратегії. За умови, що немає відомо­стей про ймовірності поведінки платника щодо сплати податків, нижня ціна гри може ви­зна­чатися за критерієм Вальда (або “максимінний критерій”). Інколи цей критерій називають критерієм перестрахування або песимізму, оскільки згідно з ним оптимальною вважається стратегія, що забезпечує максимум мінімального виграшу. Згідно з алгоритмом критерію Вальда у кожному рядку Ііплатіжної матриці спочатку знаходиться мінімальний елемент a1, a2, …, am(див. рис.1), потім серед визначених мінімальних значень виконується пошук максимального:

або .

де qi,j– значення виграшу платіжної матриці;

і – стратегії гравця І, і = 1,2, ., m;

j – стратегії гравця Р, j = 1, 2, …, n.

Таким чином, результати розрахунків за критерієм Вальда визначають стратегію Іі, при якій податковому інспектору (гравець І) буде забезпечений виграш у сумі, не меншій визначеного мінімального числа a, при будь-якій стратегії платника Рj(гравець Р). Знайдене число відображає нижню ціну гри і є одним із елементів матриці.

Верхня ціна гри може визначатися за критерієм Севіджа (критерій мінімакса), згідно з яким оптимальною вважається стратегія, при якій величина ризику у найгіршому випад­ку є мінімальною. Тобто платник податку, визначаючи свою стратегію, повинен врахову­вати, що податковий інспектор може вибрати стратегію отримання максимального виграшу. Тому платнику необхідно знайти стратегію своєї поведінки Рj, при якій його втрати у найгіршому для нього випадку будуть мінімальними.

Згідно з алгоритмом критерію Севіджа, спочатку у кожному стовпчику Рjплатіжної матриці визначається максимальний елемент b1, b2, ., bn(рис. 1), потім серед знайдених чисел вибирається мінімальне:

або .

де qi,j– значення виграшу платіжної матриці;

і – стратегії гравця І, і = 1,2, ., m;

j – стратегії гравця Р, j = 1, 2, …, n.

Критерій Севіджа надає можливість гравцю Р (платник) знайти оптимальну стратегію, при якій він втратить суму, не більшу за визначену величину b (верхня ціна гри), при будь-яких діях гравця І (інспектор). Даний критерій відображає алгоритм дії обережної особи, яка, приймаючи рішення, орієнтується на найгірші умови та наслідки і тим самим уникає ризику.

При пошуку оптимальних рішень за допомогою матричних ігор, які б задовольняли обох гравців за умови існування відомостей про ймовірність поведінки платника, можливе також застосування класичних критеріїв оптимальності – Лапласа, Бейєса, Гурвіца та ін. [3]. Для автоматизації розрахунків щодо формування оптимального плану перевірок, який визначає стратегію поведінки податкового інспектора, автором були написані програми-макроси мовою Visual Basic для роботи у середовищі MS Excel 2000 (рис. 2). Для користування макросами необхідно ввести суми виграшу для кожної зі стратегій інспектора, виділити весь діапазон і запустити макрос на виконання, натиснувши потрібну кнопку.

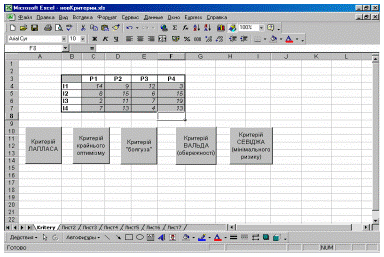
Рис. 2. Робоче вікно визначення оптимальної стратегії в MS Excel

Отже, в умовах невизначеності при адмініструванні податків можна застосовувати класичні критерії оптимальності при формуванні оптимального плану проведення доку­мен­тальних перевірок і таким чином визначити оптимальну поведінку як податкового інспек­тора, так і платника податків.

За умови, що нижня і верхня ціна матричної гри співпадають, тобто a = b, платіжна матриця має сідлову точку [14]. Сідлових точок у матриці може бути декілька, і всі вони мають одне і теж саме значення.

Стратегії гравців ІіPj, що відповідають сідловій точці, називають оптимальними, і ситуація є врівноваженою, яку ні один із гравців не буде прагнути порушити.

У тих випадках, коли нижня і верхня ціна гри мають різне значення, тобто a ¹ b, рішення матричної гри знаходиться у змішаних стратегіях, які одержують шляхом випадкового вибору чистих стратегій. Змішана стратегія гравця І позначається так:

,

де р1, р2, ., рm – ймовірності, з якими застосовуються стратегії І1, І2, ., In, причому р1 + р2 + рm = 1.

Аналогічно для гравця Р:

,

де r1, r2, ., rm – імовірності, з якими застосовуються стратегії P1, P2, ., Pn, r1 + r2 + rm = 1.

Рішенням матричної гри у змішаних стратегіях є пара оптимальних змішаних стратегій гравців і ціна гри.

За умови, що податковий інспектор проведе перевірку на підприємстві, яке внесено до плану перевірок, і не знайде порушень, він матиме програш: – q11, а якщо знайде порушення, то отримає виграш: + q12 (додатково нараховані платежі, штрафи, пеня). Програш – q11 інспектора виникає у разі нерезультативної перевірки законослухняного платника, оскільки за цей час інспектор міг би перевірити іншого платника, який не сплатив податки. При проведенні гри необхідно враховувати те, що кількість можливих документальних перевірок значно менша, ніж платників. Можливі значення виграшу при кожній парі стратегій зручно представити у вигляді платіжної матриці гри (рис. 3).