Сторінка
2

Конструювання багатомірних модальних П-регуляторів

.

При проектуванні асимптотично стійких систем керування задається точка у фазовому просторі, в яку повинна перейти динамічна система з постійним впливом на керування (4).

Обираючи зовнішні впливи для асимптотичної стійкої системи (1) з множини

,(6)

ми прагнемо забезпечити збіжність траєкторії системи до точки у фазовому просторі.

У випадку, коли

,

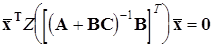то система (5) має точний розв'язок і система керування (1) досягає точки фазового простору , де

.

Якщо

,

тоді система керування (1) не досягає точки фазового простору . У цьому випадку вектор зовнішніх збурень на керування визначається з співвідношенням

. (7)

З умови (7) знаходимо, що при

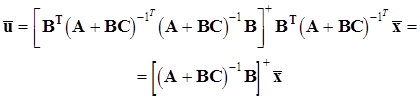(8)

досягається мінімум функціоналу (7). У цьому випадку система керування досягає точки у фазовому просторі

(9)

а квадрат похибки досягнення системою керування (1) точки має вигляд

(10)

Величину квадрата помилки досягнення (10) системи можна зменшити за рахунок зміни матриці B, тобто за рахунок вибору прикладення керуючих впливів (синтезу структури керування). Змінимо матрицю B оптимальним чином. Для цього скористаємося градієнтною процедурою визначення матриці B на k+1 - му кроці

. (11)

Для знаходження скористаємося наступною теоремою.

Теорема. Якщо матриця A+BC має повний ранг, то

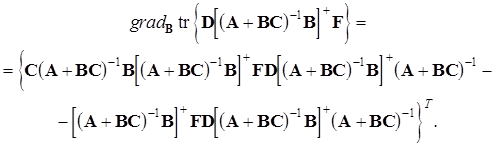
Доведення. Неважко показати, що для матриці Х, що має повний ранг, виконується співвідношення

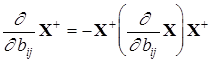. (12)

Тоді

,

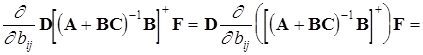
де - елемент матриці В.

Легко отримати і наступне співвідношення

.

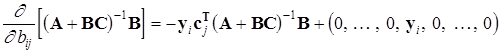Вектор-стовпчик в останній матриці розташований на j - му місці. Тут прийняті наступні позначення

.

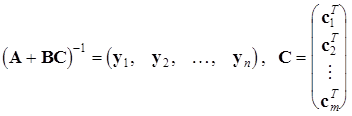Тоді

.

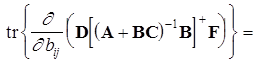
Увівши позначення

,

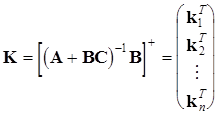одержимо

,

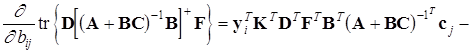
де .

Тоді

.

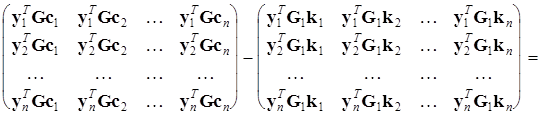
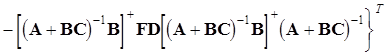Тим самим теорема доведена.

Використовуючи цей результат одержимо в явному виді наступний вираз

Приведемо необхідні умови оптимального вибору матриці В для функціоналу (10).

Запишемо приріст функціоналу (10) по вектор стовпчикам матриці В

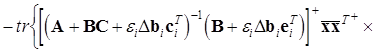(13)

+

,

,

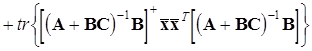де - вектор рядок матриці С, - i-й орт одиничної матриці, - приріст для вектор стовпця матриці В , . Припускаємо, що матриця A+BC має повний ранг.

Використовуючи результат робіт [7] обернену матрицю у виразі (13) можна записати в наступному виді

.

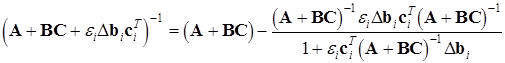Тоді формула (13) набуде вигляду

(14)

,

де вектори

,

.

Псевдообернену матрицю у виразі (14) розпишемо використовуючи математичний апарат збурення матриць [ 8 ].

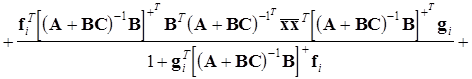(15)