Сторінка
3

Маса лінії. Координати центра ваги плоскої кривої та фігури

1.3. Обчислення моментів інерції

1. Момент інерції плоскої кривої. Момент інерції системи матеріальних точок на площині з масами відносно точки визначається так:

де

Нехай деяка крива задана рівнянням представляє собою матеріальну лінію з лінійною густиною Розіб’ємо лінію на частин довжини де і на кожній частині дуги візьмемо довільну точку з абсцисою . Ордината цієї точки буде Тоді маси цих частин будуть Наближено момент інерції лінії відносно точки буде обчислюватися за формулою Якщо функція та її похідна неперервні на , то при дана сума має границю і ця границя, що виражає визначений інтеграл, і визначає момент інерції матеріальної лінії відносно початку координат:

(10.19)

Аналогічно визначаються моменти інерції лінії відносно координатних осей і :

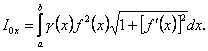(10.20)

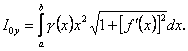(10.21)

2. Момент інерції тонкого однорідного стрижня. Розглянемо тонкий однорідний стрижень довжини і обчислимо момент інерції відносно його кінця. Розмістимо стрижень на осі . Тоді момент інерції відносно точки обчислимо за формулою (11.19)

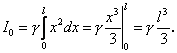
Якщо маса стрижня то і

(10.22)

Можна, наприклад, обчислити момент інерції стрижня відносно його середини

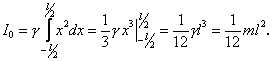
3. Момент інерції кола радіуса відносно центра. Оскільки всі точки кола знаходяться на однаковій віддалі від центра, а його маса то момент інерції кола буде

(10.23)

4. Момент інерції круга та циліндра. Розглянемо однорідний круг радіуса і масоюРозіб’ємо його на кілець і розглянемо одне із них, внутрішній радіус якого а зовнішній (рис.10.12). Маса цього кільця з точністю до нескінченно малих вищого порядку відносно буде

Момент інерції

цієї маси відносно центра дорівнює

наближено