Сторінка
2

Інтегрування з допомогою заміни змінної. Інтегрування частинами

Нехай Тоді

і

У новому інтегралі степінь величини понизився на одиницю, а це означає , що інтеграл став простішим , ніж був .

Знайдемо тепер . Маємо .

Звідси

Отже , на основі формули (8.16) одержимо

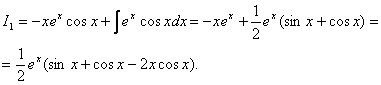
Враховуючи значення , знаходимо

.

Приклад 3.

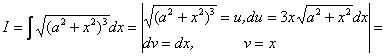
Із останньої рівності одержимо

.

Обчислимо тепер

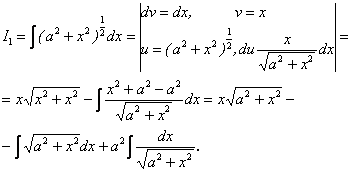
Звідси .

Остаточно з урахуванням , матимемо

Останній приклад показує, що часто інтегрування частинами приводить до мети скоріше в тих випадках, де, як це здавалось би, доцільніше застосувати інші методи . У цьому можна переконатися, спробувавши знайти первісну для функції , застосувавши наприклад , заміну змінної за формулою , про що мова буде іти пізніше.

2. Інтегрування часток

Через те , що то

. (8.18)

Користуючись цим , стають очевидними такі формули :

.

Нехай маємо , причому , де – довільне дійсне число. Тоді

.

Розглянемо інтеграл вигляду якщо , то

, (8.19)

де .

Приклади .

1..

2..

3..

Через те що , то

.

3. Заміна змінної

Нехай потрібно обчислити інтеграл причому безпосередньо первісну ми знайти не можемо, але відомо, що вона існує.

Зробимо заміну змінної в підінтегральному виразі

де неперервна функція з неперервною похідною, що має обернену функцію. Тоді і в цьому випадку має місце формула

(8.20)

Формулу (8.20) слід розуміти так, що після інтегрування в правій частині рівності замість буде підставлено його вираз через

Щоб довести рівність (8.20), потрібно довести, що похідні за від обох частин рівності рівні між собою:

Ми тут використали правило диференціювання оберненої функції.

Отже, похідні за від обох частин рівності (8.20) рівні, що й треба було довести.

Функцію потрібно вибирати так, щоби можна було обчислити інтеграл, що стоїть в правій частині рівності (8.20).

Фактично у п. 9.3.5 теж йшлося про заміну змінної, в чому можна безпосередньо переконатися .

Не можна дати універсальних замін змінних , які зводили б заданий інтеграл до простішого. Але для ряду випадків це можна здійснити. Доцільно, наприклад, в інтегралах, що містять під знаком інтеграла вирази вигляду

застосувати відповідно такі заміни змінних: або

або .

За подальшого вивчення методів інтегрування розглядатимуться інші заміни змінних .

Приклади .

1.. Підстановка зводить інтеграл до такого :

2.. Щоб позбутися експонент, доцільно скористатися такою заміною змінної .Тоді і інтеграл набере вигляду