Сторінка
2

Комплексні числа, їх зображення на площині. Алгебраїчна, тригонометрична і показникова форми комплексного числа

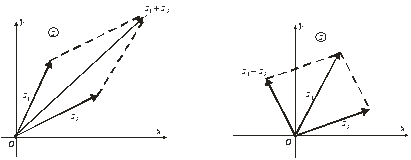Рис.8.2

спряженими. Їх добуток є дійсне число

в). Ділення. Нехай потрібно число поділити на число , тобто

Отже, в результаті ділення двох комплексних чисел одержуємо комплексне число.

г). Піднесення комплексного числа до цілого додаткового степеня здійснюється так само, як піднесення двочлена до степеня з наступною зміною степенів за формулами:

, де ціле додатне число.

д). Добування кореня порівняно легко можна здійснити лише для квадратного кореня. Для коренів вищих степенів здійснить це важко, якщо обмежуватися комплексними числами, заданими в алгебраїчній формі.

Приклад. Добути квадратний корінь із числа .

Р о з в ’ я з о к. Нехай

Тоді , де і – дійсні числа. Звідси

Розв’язавши цю систему рівнянь , одержимо

Дії додавання і множення комплексних чисел володіють переставним (комутативним), сполучним (асоціативним) і розподільчим (дистрибутивним) законами.

Приклади.

10.

20.

30.

40.

50.

1.2. Тригонометрична форма комплексного числа

Сполучимо початок координат з точкою . Довжина цього відрізка називається модулем комплексного числа, а кут , що утворює цей відрізок з додатним напрямом осі називається аргументом комплексного числа (рис.8.1). Очевидно, що аргумент дійсного числа дорівнює , а уявного -

.

Проекції відрізка на осі і відповідно дорівнюють і . Тому

(8.1)

Враховуючи формули (8.1), одержимо:

Отже,

. (8.2)

Запис комплексного числа у вигляді називають алгебраїчним, а у вигляді (8.2) - тригонометричним.

Приклади. Записати в тригонометричній формі комплексні числа:

Маємо:

Розглянемо дії з комплексними числами, заданими в тригонометричній формі.

а). Дії додавання і віднімання комплексних чисел, заданих у тригонометричній формі, можуть бути виконані так само, як і в алгебраїчній формі.

б).Множення.

(8.3)

Отже, в разі множення комплексних чисел, заданих у тригонометричній формі, їх модулі перемножуються, аргументи додаються.

в). Ділення.

(8.4)

тобто при діленні модуль діленого ділиться на модуль дільника, аргумент дільника віднімається від аргументу діленого.