Сторінка
2

Основні правила диференціювання. Таблиця похідних

Теорема. Якщо функції в точці мають похідні і , то функція також у точці має похідну і похідна дорівнює

(6.20)

Д о в е д е н н я. Надамо приросту . Тоді функції матимуть відповідно прирости , а функція - приріст

Знайдемо відношення

За умовою теореми

а , тому

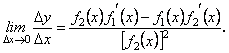
Теорему доведено.

Наслідок 1. Якщо знаменник дробу - стала величина, то

(6.21)

Наслідок 2. Якщо чисельник дробу стала величина, то

(6.22)

6. Похідна від оберненої функції.

Теорема. Нехай функція задовольняє всім умовам теореми про існування оберненої функції і в точці має похідну . Тоді обернена до неї функція у точці має також похідну: .

Д о в е д е н н я. Надамо приросту . Тоді функція дістане приріст , причому, внаслідок монотонності функції , матимемо , якщо . Тоді відношення можна записати так: Перейдемо в цій рівності до границі при . Внаслідок неперервності оберненої функції , тобто

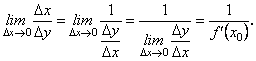
Отже, від функції в точці існує похідна:

(6.23)

Теорему доведено.

Якщо функція має похідну в довільній точці і

, то формула (6.23) справджується для цих точок

або, що те саме,

(6.24)

У формулі (6.24) похідні знаходяться за різними змінними: - похідна від до , а - похідна від до . Тому формулу (6.24) записують

(6.25)

Нижній індекс показує, за якою змінною знаходиться похідна.

Для зручності поміняємо у формулі (6.25) місцями і . Остаточно матимемо таку формулу для похідної від оберненої функції:

(6.26)

2. Похідні від елементарних функцій

Похідна від степеневої функції

Випадок натурального показника. Нехай , де - натуральне число. Тоді функція визначена на всій числовій осі. Отже, візьмемо довільну точку і надамо їй приросту . Тоді функція матиме приріст :