Сторінка
3

Закони термодинаміки і термодинамічні величини (функції) системи

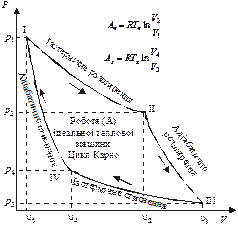
Ми не будемо тут наводити опис дослідів з «ідеальною тепловою машиною», яка забирає теплоту від нагрівача і віддає холодильнику, дослідів, які дали змогу визначити знаменитий «Цикл Карно» (рис. 16). Наведемо лише (для допитливих) кілька загальних розрахунків роботи такої ідеальної теплової машини (розрахунок роботи ізотермічного процесу вже наводився).

На першому відрізку циклу (І—ІІ) ідеальний газ за незмінної початкової температури підігрівача, від яко­го надходить тепло, виконує роботу А ізотермічного розширення:

.

Робота на цій ділянці виконується тільки за рахунок тепла, яке надходить до системи, оскільки за — внутрішня енергія газу також не змінюється. Отже, можна записати: .

На другому відрізку циклу (ІІ—ІІІ) система продовжує виконувати роботу без надходження тепла в адіабатичному процесі розширення за рахунок зменшення внутрішньої енергії .

Наступний процес циклу (ІІІ—ІV) — ізотермічне стискання газу відбувається за сталої температури холодильника за рахунок витрати зовнішньої роботи (над системою): . При цьому тепло, в яке трансформується робота стискання газу системи , цілком переходить до холодильника (внутрішня енергія системи не змінюється). Отже, .

На останньому відрізку циклу (ІV—I) для стискання газу необхідно, як і на попередньому, витратити зовнішню роботу над системою, але за адіабатичного процесу, в якому енергія роботи повністю витрачається на підвищення внутрішньої енергії температури системи. Відрізок (IV—І) завершує цикл за температури нагрівача , і система повертається до початкового стану.

Аналізуючи наведені вище розрахунки Аn і Аx та графік циклу Карно (рис. 16), зауважимо, що площа, обмежена V1 – I – II – III – V3, відображає повну роботу системи ідеального газу (Sсист.) за збільшення її об’єму від V1 до V3, а площа, обмежена V1 – I – II – III – V3, — роботу зовнішньої сили над системою — Sнадсист., зменшуючи її об’єм від V3 до V1. Це повертає систему до вихідного стану. При цьому завжди Sсист. > Sнадсист

Отже, висновок: така теплова машина може працювати безперервно, перетворюючи за кожного циклу лише частину теплової енергії, отриманої від нагрівача, в роботу, що дорівнює різниці площі Sсист. і Sнадсист., тобто площі, обмеженої графіком циклу Карно (I – II – III – IV – І).

Отже, ідеальна машина перетворила в роботу тільки частину тепла — «високотемпературну енергію» (за ), яку отримала від підігрівача , а другу частину — — «транзитом» уже як «низькотемпературну» (за ) передала холодильнику. Запишемо їх співвідношення: , або , або .

Величина h і є відомим коефіцієнтом корисної енергії (корисної дії) як штучної машини, так і природних процесів, наприклад океанічних течій від теплих широт до полярних. Як бачимо, завжди менше за одиницю. Саме це і є одним із положень другого закону термодинаміки.

Ілюстрацією дії другого закону термодинаміки в природному процесі може бути явище, яке вже було розглянуто за визначення ентальпії фотосинтезу: коефіцієнт конверсії сонячної енергії, яка надходить до зеленого листка з температурою, близькою до температури виходу, становить лише 0,02…0,04.

У техніці за рахунок більшої різниці температур робочої речовини «на вході» і «на виході», наприклад у двигунах внутрішнього згоряння чи турбінах, коефіцієнт конверсії (корисної дії) на порядок вищий.

Зі сказаного можна зробити два важливі висновки:

1) усі довільні процеси як в природі, так і в техніці, котрі зв’язані з перетворенням енергії, можуть відбуватись тільки за умов зниження її концентрованості, своєрідного розсіювання, як це має місце, коли тепло «енергії високої температури» гарячого предмета довільно «перетікає» в холодний предмет і, нагріваючи його, розсіюється в ньому, перетворюючись на «енергію нижчої температури»;

2) що нижча концентрованість енергії, то менша ефективність її перетворення (нижчий ) у впорядковану форму енергії — роботу чи внутрішню енергію хімічної структури речовини. У процесах перетворення тепла на роботу коефіцієнт конверсії () збільшується, коли більшою є різниця температур між теплом «на вході» і «на виході» робочої речовини.

За другим законом термодинаміки саме міра концентрованості енергії чи структурної впорядкованості системи в цілому визначається спеціальною функцією стану системи — ентропією (від грец. — перетворення). Ентропія позначається великою латинською літерою S. Як і відомі нам функції стану системи: тиск (P), об’єм (V), температура (T), внутрішня енергія (U) і ентальпія (H), нова функція — ентропія характеризує стан системи і її зміни.

Якщо перший закон термодинаміки називають законом збереження енергії, то другий — законом зміни ентропії.

Теорія термодинаміки показує, що зміна ентропії системи дорівнює відношенню енергії, яка передається (ізотермічно) у формі теплоти q, до абсолютної температури T, що можна записати рівнянням: