Сторінка
3
3. Теперішня вартість грошей та її визначення.
3.1. Просте дисконтування.
Дисконтування – процес, протилежний компаундируванню. Це визначення поточної вартості грошей (PV). Порядок визначення теперішньої вартості відобразимо за допомогою прикладу.
Приклад 3.
Яку суму грошей повинен покласти підприємець в банк на депозитний рахунок, якщо при відсотковій ставці 5% через років він планує отримати 127,63гр.од.
Приклади 3 і 1 мають дещо спільного : відсоткову ставку і термін, на який кладуться гроші на депозит . Але в прикладі 1 визначена сума, яку підприємець має покласти на депозит, а в прикладі 3 ми повинні визначити цю суму. В прикладі 3 задається очікувана сума через 5 років, а в прикладі 1, навпаки, саме ця сума невідома. Отже приклад 3 є оберненним до прикладу 1.
Процеси компаундирування (приклад 1) і дисконтування (приклад 3) знаходяться в тісному взаємозв”язку один з одним. Визначення поточної вартості (дисконтування) є прямою протилежністю компаундируванню. Таким чином, якщо нам відомий показник PV, то за допомогою компаундирування ми можемо розрахувати FV. Якщо ж нам відома змінна FV , то , застосувавши дисконтування, ми знайдемо PV, маючи справу з одним і тим же рівнянням, тільки в різних формах:
FVn=PV(1+і)n (4.3.)
 ( 4.8. )
( 4.8. )
Частина рівняння (4.8 ), що взята в дужки, називається фактором відсотку поточної вартості PVIF, тобто фактор відсотку поточної вартості (PVIFi,n) для і та для n - це поточна вартість 1 грошової одиниці за період n, дисконтована в майбутньому на і відсоток за кожний період.
Таким чином, якщо PVIFi,n = 1 / (1+і)n ,то
PV=FVn х (PVIFi,n)
Відповідні таблиці містять показники факторів відсотку поточної вартості для відображених і та n.
ВартістьPVIFi,n при і = 5% та n= 5 буде 0,7835.
PV = FV x (PVIFi,n) = 127 гр.од. х 0,7835 = 100 гр.од.
Відповідь: Для того, щоб отримати через 5 років суму 127,63 гр.од., необхідно при заданій процентній ставці 5% покласти на депозит сьогодні 100 гр.од.
3.2. Дисконтування анюїтетів (ренти).
Приклад 4.
Підприємцю запропонували вибір:
І варіант- трьохрічна рента з виплатою 100 гр.од. в кінці кожного року;
ІІ варіант-трьохрічна рента з виплатою 100 гр.од. на початку кожного року;
ІІІ варіант- одноразова виплата всієї суми 300 гр.од. по закінченні 3 років.
Процентна ставка - 5% в усіх випадках.
Варіант І.
Визначимо поточну вартість кожного потоку грошей, потім підсумовуємо ці показники і одержуемо PV ренти.
Рівняння для визначення теперішньої вартості анюїтетів (ренти) (4.9) :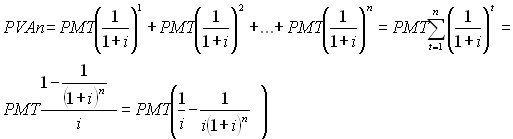
Отже, (4.9) 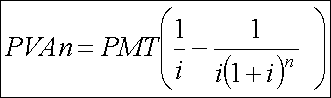
Різниця в дужках рівняння (4.9 ) називається фактором відсотку поточної вартості ренти (PVIFAi,n). В таблиці визначення теперішньої вартості анюїтетів обчислено значення цього показника для різних n та і. Рівняння матиме вигляд:
PVAn=PMT(PVIFAi,n) (4.10)
Фактор відсотку поточної вартості ренти (PVIFAi,n) - це показник анюїтетів за n-ну кількість періодів, дисконтований на і відсотків. PVIFA 5%,3 =2,7232
PVA3 = 100 гр.од. х (PVIFA 5%,3) = 100 гр.од. х 2,7232 = =272,32 гр.од.
Варіант ІІ.
При вексельній ренті кожний платіж буде зміщений вліво на 1 рік, тобто, буде дисконтуватись на 1 рік менше.
Принцип же ж вирахування такий самий, як і при звичайному анюїтеті. Оскільки виплати виконуються швидше, вексельна рента має більшу вартість, ніж звичайна. Рівняння для вексельної ренти: (4.11.)
PVA (вексельна) = РМТ х (PVIFAi,n) х (1+ і)
PVA (вексельна) = 100 гр.од. х 2,7232 х 1,05 = 285,94гр.од.
Варіант ІІІ.
За допомогою рівняння теперішньої вартості грошей і таблиці отримаємо:
![]() FVn x PVIF 5%,3 = 300 x 0,8638 = 259,14 гр.од.
FVn x PVIF 5%,3 = 300 x 0,8638 = 259,14 гр.од.
Наведені підрахунки показують, що три надходження по 100 гр.од. кожного року протягом 3 років тепер коштують лише 272,32 гр.од. за дисконта 5% при звичайній ренті або 285,94 гр.од. за цієї ж ставки відсотку при вексельній. Ці приклади демонструють суть дисконтування. Різниці між сумами
300 гр.од. - 272,32 гр.од. = 27,68 гр.од.
300 гр.од. - 285,94 гр.од. = 14,06 гр.од.
є різницями вартості грошей з часом, або загальний дисконт.
При одноразовому вкладанні 300 гр.од. на 3 роки зиск становить
300 - 259,14 = 40,86 гр.од.
Тобто прибуток від вкладання одноразово набагато більший, але і ризик з часом зростає, адже ці гроші “лежать” на депозитному рахунку всі 3 роки. Цей приклад ще раз підтверджує концепцію, що чим вище ризик, тим більша компенсація за цей ризик, і сьогодні гроші дорожчі, ніж завтра.
Таким чином, підприємець вибере той варіант вкладання грошей, який, на його думку, буде не тільки більш привабливим з точки зору розрахунків, а буде також враховувати суб”єктивні фактори: загальну ризикованість операції; репутацію банку, що відкриває депозитний рахунок; можливості швидкого та ефективного реінвестування отриманих грошей, тощо.
4. Оцінка майбутньої та теперішньої вартості грошей з врахуванням фактору інфляції.
Методичний інструментарій оцінки вартості грошових коштів з врахуванням фактору інфляції дозволяє здійснювати розрахунки як майбутньої, так і поточної їх вартості з відповідною «інфляційною складовою». В основі здійснення цих розрахунків лежить реальна відсоткова ставка, що формується.
При оцінці майбутньої вартості грошей з врахуванням фактору інфляції використовується формула (4.12) :
FV=PVx[(1+i)x(1+ТІ)]n, де
ТІ- прогнозований темп інфляції, вираженний десятковим дробом.
При оцінці теперішньої вартості грошей з врахуванням фактору інфляції використовується наступна формула (4.13):
![]()
Література
1. Бланк И.А. Основы финансового менеджмента. Т.1,2.- К.:Ника-центр,1999.
2. Брігхем Є.Г. Основи фінансового менеджменту. К., Молодь, 1997, стор. 251 -297.
3. 3 Ковалев В.В. Финансовый анализ: Управление капиталом. Выбор инвестиций. Анализ отчетности. М., Финансы и статистика, 1996, стор.156-171.
4. Нікбахт Е., Гроппелі А. Фінанси. К., Вік, Глобус, 1992, стор. 38 -58.
5. Фінансовий менеджмент: Навч.-метод. Посібник для самост. Вивч. Диск. / К.: КНЕУ, 2001, стор. 99-127.
