Сторінка
1

Визначення очікуваної дохідності та ризику портфеля

Портфель, який формує інвестор, складається з кількох активів, кожний з яких має свою очікувану дохідність.

Очікувана дохідність портфеля цінних паперів визначається як середньозважена очікувана дохідність активів, які входять до його складу, а саме:

,

де E(rp) — очікувана дохідність портфеля;

E(r1), E(r2), E(rn) — очікувана дохідність відповідно першого, другого та n-го активів;

W1, W2, Wn — питома вага в портфелі першого, другого та n-го активів.

Формула для визначення очікуваної дохідності портфеля може бути записана в компактнішому вигляді:

,

де Wі — питома вага активу в портфелі.

Питома вага активу в портфелі розраховується як відношення його вартості (Рі) до вартості всього портфеля (Рn):

.

Сума питомої ваги всіх активів, які входять до складу портфеля, завжди дорівнює одиниці.

Запишемо формулу визначення очікуваної дохідності активу в загальному вигляді.

,

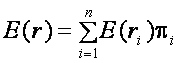де E(r) — очікувана дохідність активу;

E(ri) — очікувана дохідність активу в і-му випадку;

pі — імовірність отримання дохідності в і-му випадку.

Коли інвестор купує актив, він орієнтується не тільки на значення його очікуваної дохідності, але й на рівень його ризику. Очікувана дохідність — це певна величина, яку очікує отримати інвестор, наприклад 15 %. Однак на практиці вона може бути більшою або меншою 15 %. Отже, ризик інвестора полягає в тому, що він може отримати результат, який відрізняється від очікуваного. Якщо фактична дохідність буде більшою 15 %, то це плюс для інвестора. На практиці як ступінь ризику використовують показники дисперсії та стандартного відхилення. Вони показують, наскільки та з якою ймовірністю фактична дохідність активу може відрізнятися від очікуваної, тобто середньої. Ці параметри враховують відхилення як у бік збільшення, так і зменшення дохідності порівняно з очікуваним значенням.

Дисперсія визначається відхиленням можливих норм дохідності.

,

де s2 — дисперсія дохідності активу;

n — кількість періодів спостереження;

— середня дохідність активу;

ri — дохідність активу в і-му періоді.

Середня дохідність активу визначається як середнє арифметич­не дохідностей активів за періоди спостереження.

.

Стандартне відхилення визначається як квадратний корінь з дисперсії.

.

Очікуваний ризик портфеля — сполучення стандартних відхилень (дисперсій) активів, які входять до його складу. Однак на відміну від очікуваної дохідності портфеля, його ризик не обов’яз­ково є середньозваженою величиною стандартних відхилень (дисперсій) дохідностей активів. Справа в тому, що різні активи можуть по-різному реагувати на зміни кон’юнктури ринку. У результаті стандартні відхилення (дисперсії) дохідності різних активів у певних випадках будуть гасити один одного, що приведе до зниження ризику портфеля, який залежить від того, у якому напрямі змінюються дохідності активів за зміни кон’юн­ктури ринку й наскільки.

Для визначення ступеня взаємозв’язку й напряму зміни дохідностей використовують показник коваріації, який показує, до якої міри дві змінні разом змінюються в часі. Аналіз портфеля зазвичай звертає увагу на коваріації норм дохідності. Позитивна коваріація означає, що норми дохідності двох інвестицій мають тенденцію змінюватись в одному напрямі за певний час. Від’ємна ж показує, що норми дохідності двох інвестицій мають тенденцію змінюватись у різних напрямах за певний час.

Для двох активів (А і В) коваріація норм дохідності визначається в такий спосіб:

,

де COVА, В — коваріація дохідності активів А і В;

— середня дохідність активу А за n періодів;

— середня дохідність активу В за n періодів;

rAі — дохідність активу А в і-му періоді;

rBі — дохідність активу В в і-му періоді;

n — кількість періодів, за які реєструвалась дохідність активів А і В.

Щоб обчислити кореляцію між двома акціями або іншими інвестиціями, потрібно обчислити такі математичні значення:

1) дисперсію для доходу кожного активу;

2) стандартне відхилення для доходу кожного активу;

3) коваріацію між двома доходами цих активів.

Іншим показником ступеня взаємозв’язку змін дохідностей двох активів є коефіцієнт кореляції, який розраховується за такою формулою:

,

де CORRA, B — коефіцієнт кореляції дохідності активів А і В;

СОVА,В — коваріація дохідності активів А і В;

sА — стандартне відхилення дохідності активу А;

sВ — стандартне відхилення активу В.

Коефіцієнт кореляції може змінюватися в межах від –1 до +1. Якщо це означає, що між ними існує позитивне лінійне відношення, то доходи двох акцій змінюються разом лінійним способом. Якщо це означає негативне лінійне відхилення між двома серіями доходу, норма дохідності за одним активом буде на певну величину вищою від середнього значення, а за іншим активом — нижчою від нього. За нульового значення коефіцієнта кореляції між дохідностями активів немає.

Ризик портфеля, який складається з двох активів, розраховується за такою формулою:

,

де — ризик (дисперсія) портфеля;

WA — питома вага активу А в портфелі;

WВ — питома вага активу В в портфелі;

COVA, B — коваріація дохідностей активів А і В.

Оскільки

,

то формулу

можна переписати, скориставшись коефіцієнтом кореляції:

,

.

Якщо один портфель (актив) має вищий рівень дохідності, ніж інші портфелі (активи), за того самого ризику або нижчий ризик за тієї самої дохідності, то його називають домінуючим портфелем (активом). На рис. 12.1 домінуючим портфелем буде Р2, оскільки і Р1, і Р2 мають однаковий ризик (s1), але дохідність портфеля Р2 (r2) більша ніж дохідність портфеля Р1 (r1). Аналогічно портфель Р2 буде домінуючим відносно Р3, оскільки обидва вони мають однакову дохідність (r1), але ризик портфеля Р2 (s2) менший за ризик портфеля Р3 (s3). У той самий час, якщо порівняти портфелі Р1 і Р4, то не можна сказати, який з них є домінуючим відносно іншого, оскільки вони мають різні значення як очікуваної дохідності, так і ризику. Портфель Р4 має порівняно з портфелем Р1 як вищу очікувану дохідність, так і більший ризик.