Сторінка
3

Визначення очікуваної дохідності та ризику портфеля

Є підстави передбачити, що крива байдужості азартного інвестора (рис. 12.3) матиме негативний нахил, тобто він віддасть перевагу портфелю, який знаходиться вище і правіше від інших (точка В). Це пояснюється бажанням отримати максимальний дохід за найбільшого ризику.

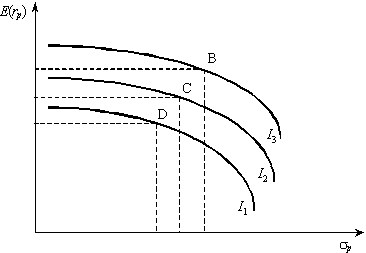
Рис. 12.3. Графік кривих байдужості азартного інвестора

Випадок нейтральності до ризику знаходиться між випадками уникнення ризику та азартності. Нейтральному інвестору все- одно — брати участь у «чесній грі» чи ні. Це означає, що ризик не є важливим для інвестора за оцінки портфеля. Крива байдужості такого інвестора буде горизонтальною лінією (рис. 12.4). Він віддає перевагу портфелям, розташованим на кривих байдужості якнайвище, тобто таким, які мають максимальну очікувану дохідність (точка В).

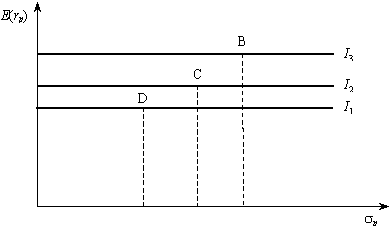
Рис. 12.4. Графік кривих байдужості інвестора, нейтрального до ризику

Хоча побудова кривих байдужості значно звужує поле формування інвестиційного портфеля, вона не дає можливості обрати найефективніший його варіант, оскільки існує множина таких варіантів, що відповідають цілям конкретного інвестора. Наблизитися до вирішення цього завдання дає змогу сформульована Г. Марковіцем «теорема про ефективну множину», яка фіксує модель поведінки інвестора в процесі формування портфеля так: «Інвестор обирає свій оптимальний варіант портфеля з їх множини, кожен з яких:

1) забезпечує максимальне значення рівня очікуваної дохіднос­ті за будь-якого певного рівня ризику;

2) забезпечує мінімальне значення рівня ризику за будь-якого певного рівня дохідності».

Сукупність варіантів портфелів, які забезпечують досягнення заданих показників, характеризується термінами «ефективна мно­жина» або «границя ефективності портфелів».

Якщо об’єднати в портфель деяку кількість активів, кореляція дохідності яких знаходиться в діапазоні від –1 до +1, то залежно від їх питомої ваги можна побудувати множину портфелів з різними параметрами ризику й дохідності, які розташовані в межах фігури АВСDE, як показано на рис. 12.5.

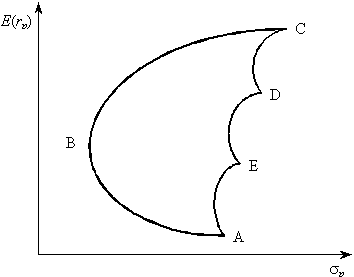
Рис. 12.5. Ефективна множина портфелів

Раціональний інвестор буде намагатися мінімізувати свій ризик і збільшити дохідність. Тому з усіх можливих портфелів, які представлено на рис. 12.5, він віддасть перевагу тільки тим, які розташовано на відрізку ВС, оскільки вони є домінуючими відносно портфелів з тим самим рівнем ризику або з такою самою дохідністю. Набір портфелів на відрізку ВС називають ефективною множиною, або границею ефективності портфелів. Ефективна множина портфелів складається з домінуючих портфелів.

Щоб визначити границю ефективності портфелів, потрібно розрахувати питомі ваги активів, які входять до складу портфеля, за яких мінімізується значення стандартного відхилення для кожного рівня дохідності, тобто

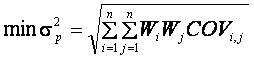
за умови, що

і .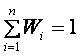

Техніка створення ефективних портфелів Марковіца з великих груп цінних паперів потребує великої кількості розрахунків. Для портфеля з цінних паперів є 12 окремих обчислень коваріацій. Отже, для портфеля з 50-ти цінних паперів є 1225 коваріацій, що мають бути обчислені. Для 100 цінних паперів — 4950.

Ці розрахунки проводяться за допомогою комп’ютера. Крім того, щоб визначити портфель, який мінімізує ризик для кожного рівня доходу, необхідний такий математичний метод, як квадратичне програмування.

Тепер розглянемо портфель, який складається з безризикованого й ризикованого активів. Як було зазначено вище, ризик портфеля, до якого входять два активи, визначається за такою формулою:

.

Оскільки один актив є безризикованим, наприклад В, а інший ризикованим (А), то sВ = 0 і COVА, В = 0. Тому формула для цього випадку набуває такого вигляду:

,

.

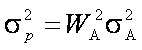Отже, ризик цього портфеля дорівнює добутку ризику ризикованого активу та його питомої ваги в портфелі. Очікувана дохідність визначається за такою формулою:

.

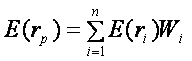Графічно залежність між очікуваними ризиком і дохідністю являє собою пряму лінію, як показано на рис. 12.6. Змінюючи питому вагу активу А, інвестор може побудувати портфель з різними характеристиками ризику й дохідності; усі вони розташовуються на відрізку АВ, і їхній ризик пропорційний питомій вазі активу А. Такий випадок можна розглядати як купівлю інвестором ризикованого активу А, а також надання кредиту (купівля активу В), оскільки придбання активу без ризику — це кредитування емітента. Тому портфелі на відрізку АВ (наприклад, портфель С) є кредитними.

Інвестор може побудувати свою стратегію не тільки на основі надання кредиту, а й позичаючи кошти під нижчий процент, ніж очікувана дохідність ризикового активу А, щоб придбати на них актив А і отримати додатковий дохід. У цьому випадку інвестор отримує можливість сформувати будь-який портфель, який розташовується на продовженні прямої АВ за межами точки А, наприклад портфель D. Йому властиві вищі ризик та очікувана дохідність. Оскільки для формування портфеля D інвестор позичає кошти, то його називають позиковим портфелем. Отже, усі портфелі, які знаходяться на продовженні прямої АВ вище від точки А, називають позиковими.

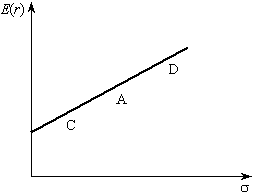
Рис. 12.6. Варіанти портфелів, які складаються з ризикованого й безризикованого активів

Використовуючи фінансовий важіль, теоретично інвестор може отримати будь-яке високе значення очікуваної дохідності. Такі портфелі розташовуються на продовженні прямої АВ вище від точки А. Однак на практиці вкладник зіткнеться з двома проблемами, які обмежать очікувану дохідність його стратегії: