Сторінка
2

Інтегрування раціональних дробів та виразів, що містять ірраціональності

Знаменники в обох частинах рівні, тому і чисельники повинні бути рівні, тобто

х = (Ах + В)(х - 1) + С(х2 + 1) (А + С)х2 + (В - А) + С - В (5)

Рівність (5) можлива лише тоді, коли коефіцієнти при одна­ковому степеню х в обох частинах рівності однакові, тобто

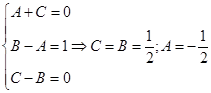
Отже, розклад (4) тепер приймає вигляд

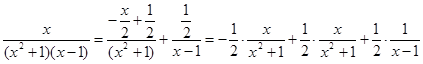
Інтегруючи цю рівність, одержимо

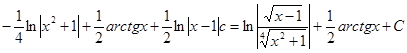
2. Інтегрування виразів, що містять ірраціональності

При інтегруванні виразів, що містять дробові степені змінної інтегрування (тобто ірраціональності), методом відстановки зводять підінтегральну функцію до раціонального дробу. Розг­лянемо декілька випадків.

1. Підінтегральна функція є раціональним дробом відносно , де дробове число. У цьому випадку вводять нову змінну t = х1/q , де q — спільний знаменник дробових показників степеня змінної х.

Приклад 2. Знайти

Розв'язування. Маємо:

Спільний знаменник дробових показників степенів 1/2, 4/3, 5/4 змінної х дорівнює 12. Тому зробимо підстановку t = х1/12, х = t12, dx = 12t11dt i ми одержуємо:

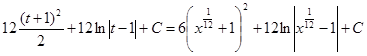
2. Підінтегрований вираз містить дробові степені лінійного двочлена (ах+b). У цьому випадку доцільно зробити підстанов­ку t = (ах + b)1/q, де q —спільний знаменник дробових показ­ників степенів двочлена.

Приклад 3. Знайти

Розв'язування. Нехай t = (х + 1)1/2, х + l = t2, x = t2- 1, dx = 2tdt

Тому