Сторінка
2

Наближене розв’язування рівнянь: графічне відокремлення коренів, методи проб, хорд і дотичних

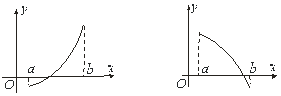Рис.7.2 Уточнимо корінь рівняння способами хорд і дотичних. Зміст цих способів полягає в тому, що точка перетину кривої з віссю замінюється точкою перетину з віссю відповідно хорди ( в методі хорд ) і дотичної (в методі дотичних ).

7.2.1.Метод хорд Напишемо рівняння хорди:

і покладемо в нього . Знайдемо - абсцису точки перетину хорди з віссю :

Із умов, яким задовольняє функція , випливає, що Позначимо через точку кривої , відповідну (рис.7.3). Розглянемо хорду та знайдемо її точку перетину з віссю

при цьому Продовжуючи цей процес, означимо послідовність :

Послідовність - монотонна, обмежена і збіжна. Можна довести, що . Абсолютна похибка -го наближення оцінюється за нерівністю

де - найменше значення на відрізку Тому можна зупинити процес тоді, коли стане менше допустимої похибки результату.

3. Метод дотичних Проведемо дотичну до кривої в точці (рис.7.4 ). Саме в цій точці збігаються знаки функції та (дотична до кривої в точці може перетнути вісь за межами відрізка ).

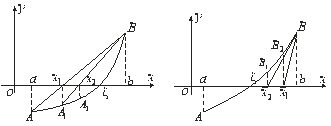Рис.7.3 Рис.7.4 Знайдемо точку перетину цієї дотичної з віссю . Рівняння дотичної запишемо у вигляді:

. Покладемо в цьому рівнянні . Знайдемо - абсцису точки перетину дотичної з віссю :

, Значенню відповідає точка кривої . Абсциса точки перетину дотичної до кривої в точці з віссю буде

. Продовжуючи цей процес, знайдемо

. Послідовність- монотонна і обмежена. Можна довести, що . Абсолютна похибка -го наближення може бути оцінена за нерівністю

. Якщо потрібно обчислити корінь рівняння з абсолютною похибкою, не більшою від заданого числа то закінчуємо обчислення при

. Зауваження. На практиці часто використовують обидва методи. Одним методом одержують наближення шуканого кореня з нестачею, а другим – з надлишком. Яким саме методом одержується наближення кореня з нестачею, а яким – з надлишком, залежить від функції . Якщо врахуємо, що кожна послідовність та - монотонна, то легко знаходити корінь з заданою точністю, оскільки знаки, що збігаються в наближеннях та (в наближеннях та ) є правильними.